За каждое правильно выполненное задание начисляется два балла, в противном случае – ноль баллов.
I. Пусть 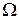 – достоверное событие, а
– достоверное событие, а 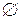 – невозможное событие. Верно ли утверждение?
– невозможное событие. Верно ли утверждение?
1. Для любого события 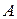 справедливо равенство:
справедливо равенство: 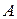 ∙
∙ 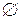 =
= 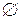 .
.
2. Для любого события 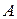 справедливо равенство:
справедливо равенство: 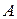 ∙
∙ 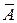 =
= 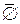 .
.
3. 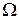 +
+ 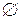 =
= 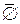 .
.
4. Существует событие 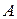 такое, что
такое, что 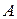 +
+ 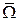 =
= 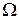 .
.
II. Пусть A, B – случайные события и P(A), P(B) – их вероятности, тогда
5. P(A+B)=P(A)+P(B) 6. P(AB)=P(A)P(B) 7. AÌ B Þ P(A+B)=P(A) 8. 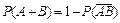
III. Справедливы утверждения для ненулевых вероятностей произвольных событий: A, B и Ω – достоверного события
9. P(A+B)bP(A)+P(B) 10. P(Ω)r 0 11. P(Ω)=0 12. P(A|B)=P(AB)P(B)
IV. В урне 4 белых шара, 3 чёрных и 2 красных. Из урны наудачу выбирается один шар. Рассмотрим случайные события A, B, C, состоящие в том, что вынут: A – белый; B – чёрный и C – красный шар. Верно утверждение.
13. 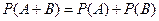 14.
14. 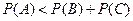
15. 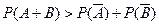 16.
16. 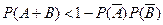
V. Пусть X, Y – случайные величины, тогда:
17. M(X+Y)=M(X)+M(Y) 18. M(XY)=M(X)M(Y)
19. D(X+Y)=D(X)+D(Y) 20. D(XY)=D(X)D(Y)
VI. Пусть 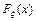 – функция распределения случайной величины ξ, тогда:
– функция распределения случайной величины ξ, тогда:
21. 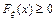 22.
22. 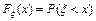 23.
23. 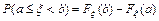 24.
24. 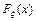 – возрастающая ф-ция.
– возрастающая ф-ция.
VI. Пусть 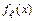 – функция плотности распределения случайной величины ξ, тогда:
– функция плотности распределения случайной величины ξ, тогда:
25. 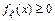 26.
26. 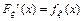 27.
27. 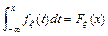 28.
28. 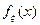 – возрастающая ф-ция.
– возрастающая ф-ция.
VII. Непрерывная случайная величина X задана имеет равномерное распределение и отлична от нуля на отрезке [2;10]. Тогда
29. P(X>3)=7/8 30. P(6<X<11)=5/8 31. M(X)=6 32. D(X)= 3
IX.
X.
 2015-09-06
2015-09-06 1877
1877







