Изображение многогранников в параллельной проекции

Лемма. Пусть четырехугольники A ₁ B ₁ C ₁ D ₁ и ABCD, лежащие соответственно в плоскостях σ₁ и σ, аффинно-эквивалентны. Здесь учитывается порядок вершин, в котором записаны данные четырехугольники, т.е. предполагается, что существует аффинное отображение f: σ→σ₁, такое, что А ₁= f (A), B ₁= f (B ₁), C ₁= f (С) и D ₁= f (D). Тогда существует такая плоскость σ₀, что проекция четырехугольника A ₁ B ₁ C ₁ D ₁ на эту плоскость по направлению вектора, ортогонального к плоскости σ подобна четырехугольнику АВСD.

Теорема (Польке - Шварца). Вершины любого четырехугольника ABCD плоскости σ, заданные в определенном порядке, могут служить изображением аффинного репера, равного данному реперу R *=(A *, В *, С *, D *).

На прямых А * С * и B * D * возьмем точки М * и N * так, чтобы (А * С *, М *)=(АС, Е) и (B * D *, N *)=(BD, Е). Здесь Е - точка пересечения прямых АС и BD (рис. 3.1). Проведем какую-нибудь плоскость σ₁, перпендикулярную к прямой М * N *, и рассмотрим ортогональную проекцию A ₁ B ₁ C ₁ D ₁ репера R * на эту плоскость. Точки М * и N * проектируются в одну и ту же точку Е ₁ (рис. 3.1). Так как (A ₁ C ₁, E ₁)=(A * С *, M *)=(АС, Е) и (B ₁, D ₁, E ₁)=(B * D *, N *)=(BD, E), то четырехугольники A ₁ B ₁ C ₁ D ₁ и ABCD аффинно-эквивалентны (теорема 2).

Рис. 3.1

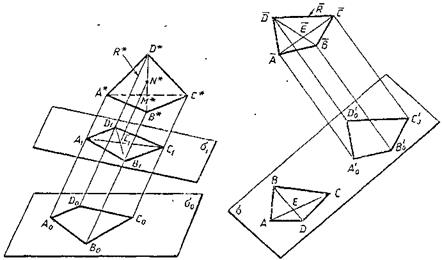
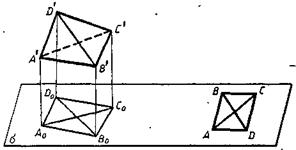
Рис. 3.2

По предыдущей лемме существует такая плоскость σ₀, что проекция A ₀ B ₀ C ₀ D ₀ четырехугольника A ₁ B ₁ C ₁ D ₁ на эту плоскость по направлению вектора подобна четырехугольнику ABCD. Заметим, что точки А *, А ₁, A ₀ лежат на одной прямой, перпендикулярной к плоскости σ₁, поэтому точка A ₀ - параллельная проекция точки А * на плоскость σ₀ по направлению вектора 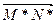. Аналогично точки В ₀, С ₀ и D ₀ являются параллельными проекциями точек В *, С * и D * на эту же плоскость, т.е. четырехугольник A ₀ B ₀ C ₀ D ₀- параллельная проекция репера R * на плоскость σ₀.

Рассмотрим какое-нибудь движение трехмерного пространства, в котором плоскость σ₀ переходит в плоскость σ. Обозначим через 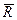=(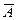, , 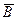, 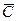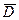) образ репера R *, а через 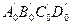образ четырехугольника A ₀ B ₀ C ₀ D ₀ в этом движении. Мы видим, что проекция репера R на плоскость σ подобна данному четырехугольнику ABCD, т.е. ABCD - изображение репера 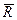, равного данному реперу R *.

Рассмотрим теперь на плоскости σ изображения некоторых многогранников. Предположим, что ни одна из плоскостей граней многогранника не параллельна направлению проектирования.

В теории изображений учитываем, что многогранник полностью определяется своей поверхностью, составленной из многоугольников (грани многогранника). Эта поверхность ограничивает многогранник как геометрическое тело. Под изображением многогранника будем понимать фигуру, состоящую из изображений всех его граней (или, что, по существу, то же самое, всех его ребер). Для большей наглядности невидимые ребра многогранника изображают пунктирными линиями.

а) Тетраэдр. Пусть А'В'С'D' - тетраэдр-оригинал. A ₀, B ₀, С ₀, D ₀ - проекции его вершин, а А, В, С и D - изображения его вершин (рис. 3.2). Тогда фигура, состоящая из треугольников ABC, ABD, ACD и BCD, и будет изображением этого тетраэдра. Другими слова ми, изображением тетраэдра A'B'C'D' является фигура, состоящая из всех сторон и диагоналей четырехугольника ABCD.

Рис. 3.3

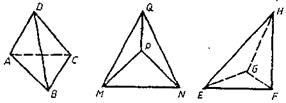
Из теоремы Польке - Шварца следует вывод: вершины произвольного четырехугольника плоскости σ могут служить изобра­жением вершин тетраэдра, равного данному тетраэдру. Поэтому если задан тетраэдр, то для его изображения достаточно начертить на плоскости σ произвольный четырехугольник и провести его диагонали. На рисунке 3.3 изображено несколько тетраэдров. Для большей наглядности невидимые линии изображены пунктиром. Следует отметить, что на этом рисунке четырехугольник ABCD выпуклый, а четырехугольники MNPQ и EFGH невыпуклые.

б) Параллелепипед. Изображением параллелепипеда (в том числе прямоугольного параллелепипеда, куба) является фигура, состоящая из трех пар параллелограммов, причем в каждой паре один получается из другого параллельным переносом (рис. 3.4).

Для того чтобы построить изображение данного параллелепипеда A ₀ B ₀ C ₀ D ₀ 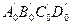, следует учесть, что, например, точки A ₀ B ₀ D ₀ и являются вершинами тетраэдра (рис. 3.5, а), поэтому по теореме Польке - Шварца в качестве их изображений можно выбрать вершины произвольного четырехугольника ABDA' плоскости σ. Изображения же остальных вершин получаются построением с учетом того, что изображениями граней параллелепипеда являются параллелограммы (рис. 3.5, б).

в) Призма. Изображением n -угольной призмы на плоскости σ является фигура, состоящая из двух равных n -угольников (один получается из другого параллельным переносом), изображающих основания призмы, и n параллелограммов, для каждого из которых противоположными сторонами являются изображения параллельных сторон оснований (рис. 3.6).

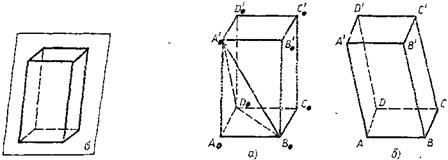
Рис. 3.4

Рис. 3.5

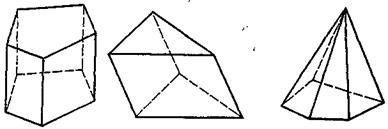
Рис. 3.6

Рис. 3.7

Построение изображения данной призмы выполняется аналогично построению изображения параллелепипеда. Основания призмы изображаются на чертеже с учетом правил изображений плоских многоугольников.

г) Пирамида. Изображением пирамиды является фигура, состоящая из многоугольника, изображающего основание пирамиды-оригинала, и нескольких треугольников с общей вершиной, изображающих боковые грани пирамиды (рис. 3.7).

Для построения изображения данной пирамиды следует учесть, что по теореме Польке - Шварца за изображение вершины пирамиды и трех вершин основания можно взять вершины произвольного четырехугольника плоскости σ. Тогда изображения остальных вершин основания и всех ребер получаются построением с учетом правил изображений плоских многоугольников. Например, на рисунке 3.8 изображена четырехугольная пирамида, основанием которой является прямоугольник. Точки S, А, В и D являются вершинами произвольного четырехугольника, а точка С построена так, чтобы ABCD был параллелограммом.

Замечание. Иногда приходится строить более сложные многогранники. Для построения такого многогранника аналогично предыдущему за изображение четырех вершин (трех вершин, принадлежащих одной грани, и еще одной вершины смежной грани) принимают вершины произвольного четырехугольника плоскости σ, тогда изображения остальных вершин и всех ребер получаются по построению. Например, на рисунке 3.9 дано изображение более сложного многогранника.

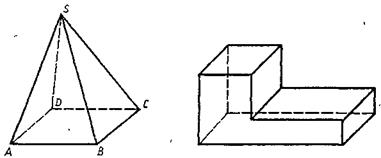
Рис. 3.8

Рис. 3.9