1. Введем в пространстве аффинную систему координат 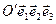 и рассмотрим соответствующий репер R' =(O',
и рассмотрим соответствующий репер R' =(O', 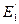 ,
, 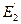 ,
, 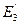 ), где
), где 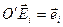 , i =1, 2, 3. Произвольная точка М' пространства в этом репере имеет координаты х, у, z, которые определяются равенством
, i =1, 2, 3. Произвольная точка М' пространства в этом репере имеет координаты х, у, z, которые определяются равенством 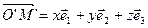 , или
, или
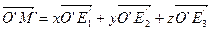 .
.
(1)
Рассмотрим координатную ломаную 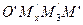 точки М'. Здесь
точки М'. Здесь 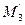 - проекция точки М' на плоскость Oху по направлению оси
- проекция точки М' на плоскость Oху по направлению оси 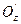 , а
, а 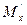 - проекция точки
- проекция точки 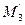 на ось
на ось 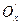 по направлению оси
по направлению оси 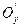 (рис. 4.1, а).
(рис. 4.1, а).
Возьмем теперь плоскость σ изображений, выберем направление проектирования так, чтобы оно не было параллельно координатным плоскостям, и спроектируем на эту плоскость репер R' и координатную ломаную точки М'. Подвергнув затем плоскость σ преобразованию подобия, получим на ней изображение репера R' и координатной ломаной точки М': R =(О, Е 1, Е 2, Е 3), ОМ х М 3 М (рис. 4.1, б). Докажем, что
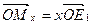 ,
, 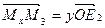 ,
, 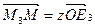 , (2)
, (2)
где x, y, z - координаты точки M' в репере R'.
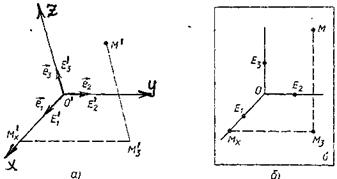
Рис. 4.1
В самом деле, по равенству (1) 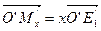 , поэтому
, поэтому 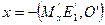 . При параллельном проектировании и подобии сохраняется простое отношение трех точек, поэтому
. При параллельном проектировании и подобии сохраняется простое отношение трех точек, поэтому 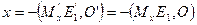 , т.е.
, т.е. 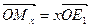 . Аналогично получаем остальные два равенства в отношениях (2).
. Аналогично получаем остальные два равенства в отношениях (2).
Из равенств (2) следует важный вывод: если на плоскости σ дано изображение R репера R', то можно построить изображение М любой точки М' по ее координатам в репере R'. Для этого на плоскости σ сначала по формулам (2) строим векторы 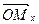 ,
, 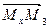 ,
, 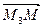 , а затем строим точку М, используя равенство
, а затем строим точку М, используя равенство 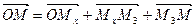 .
.
Умея указанным образом строить изображения точек пространства, мы можем строить и изображения пространственных фигур. Этот метод называется методом аксонометрического проектирования (аксонометрия - измерение по осям) и широко применяется в инженерно-технической практике, Точку O называют началом аксонометрической системы координат, а оси ОЕ 1, ОЕ 2, ОЕ 3 - аксонометрическими осями.
Возникает вопрос: можно ли вершины произвольного четырехугольника плоскости σ, заданные в определенном порядке, рассматривать как изображение данного аффинного репера R' пространства? Ответ на этот вопрос дает теорема Польке - Шварца: вершины любого четырехугольника плоскости изображений, заданные в определенном порядке, могут служить изображением аффинного репера, равного данному реперу R. Другими словами, на плоскости изображений начало O и аксонометрические оси ОЕ 1, ОЕ 2, ОЕ 3 можно выбрать произвольно при условии, что O, Е 1, Е 2, Е 3- точки общего положения.
2. Пусть R =(О, Е 1, Е 2, Е 3)- изображение аффинного репера R' пространства, а М, М 1, М 2 и М 3 - изображения данной точки М' и ее проекций 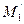 ,
, 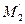 и
и 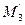 на координатные плоскости по направлениям соответствующих координатных осей (рис. 4.2). Точку М называют аксонометрической проекцией точки М' а точки M 1, M 2 и М 3 - вторичными проекциями этой точки. Отметим, что если на плоскости σ задана точка М и одна из точек М 1, М 2, М 3 (например, М 3), то точка М' в пространстве вполне определяется. В самом деле, по точкам М и М 3 мы сможем восстановить ломаную ОМ x М 3 М и с ее помощью по формулам (2) найти координаты х, у, z точки М' в репере R'. Таким образом, точку М' пространства мы можем задать на плоскости σ с помощью двух точек (М, М 3), которые расположены так, что прямые MM 3 и Oz параллельны или совпадают (риc. 4.3). Обратно: любые две точки (М, М 3) плоскости σ расположенные так, что прямые MM 3 и Oz параллельны или совпадают, определяют в пространстве некоторую точку М' для которой М - аксонометрическая проекция, а М 3 - вторичная проекция. Точки М и М 3. совпадают тогда и только тогда, когда точка М' лежит в плоскости О' ху. Этот способ и применяется в аксонометрии для задания точек пространства на плоскости изображении. При этом обычно вместо предложения «В пространстве дана точка М', аксонометрическая проекция которой на плоскость σ есть М, а вторичная проекция - точка М 3» говорят кратко: «Дана точка (М, М 3)».
на координатные плоскости по направлениям соответствующих координатных осей (рис. 4.2). Точку М называют аксонометрической проекцией точки М' а точки M 1, M 2 и М 3 - вторичными проекциями этой точки. Отметим, что если на плоскости σ задана точка М и одна из точек М 1, М 2, М 3 (например, М 3), то точка М' в пространстве вполне определяется. В самом деле, по точкам М и М 3 мы сможем восстановить ломаную ОМ x М 3 М и с ее помощью по формулам (2) найти координаты х, у, z точки М' в репере R'. Таким образом, точку М' пространства мы можем задать на плоскости σ с помощью двух точек (М, М 3), которые расположены так, что прямые MM 3 и Oz параллельны или совпадают (риc. 4.3). Обратно: любые две точки (М, М 3) плоскости σ расположенные так, что прямые MM 3 и Oz параллельны или совпадают, определяют в пространстве некоторую точку М' для которой М - аксонометрическая проекция, а М 3 - вторичная проекция. Точки М и М 3. совпадают тогда и только тогда, когда точка М' лежит в плоскости О' ху. Этот способ и применяется в аксонометрии для задания точек пространства на плоскости изображении. При этом обычно вместо предложения «В пространстве дана точка М', аксонометрическая проекция которой на плоскость σ есть М, а вторичная проекция - точка М 3» говорят кратко: «Дана точка (М, М 3)».
3. Рассмотрим теперь изображения прямых и плоскостей на плоскости σ. Из соображений наглядности будем предполагать, что направление проектирования не параллельно рассматриваемым прямым и плоскостям. Поэтому аксонометрическая проекция любой прямой есть прямая линия, а аксонометрическая проекция плоскости - вся плоскость σ.
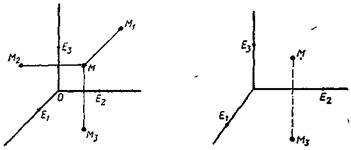
Рис. 4.2
Рис. 4.3
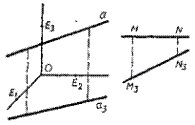
Рис. 4.5
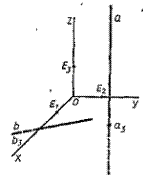
Рис. 4.6
Прямая а' пространства на плоскости изображений задастся двумя ее точками (М, М 3) и (N, N 3) или аксонометрической проекцией а и вторичной проекцией а 3. На рисунке 4.5 изображены прямые (а, а 3) и (MN, M 3 N 3). Если прямая а' не параллельна оси O'z' то ее вторичная проекция а 3 есть прямая, в противном случае - точка. На рисунке 36 изображена прямая а', параллельная оси О'z'. Мы видим, что ее аксонометрическая проекция а - прямая, параллельная аксонометрической оси Oz, a вторичная проекция а 3 - точка. Сама ось O'z на плоскости, а задается парой (Oz, О). Отметим, что аксонометрическая и вторичная проекции прямой совпадают тогда и только тогда, когда прямая а' в пространстве лежит в плоскости O'x'y' (прямая (b, b 3) на рис. 4.6).
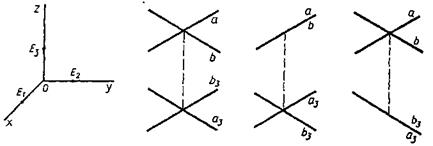
Рис. 4.7
Выясним взаимное расположение двух прямых (а, a 3) и (b, b 3), не параллельных оси O'z. Эти прямые пересекаются тогда и только тогда, когда они имеют единственную общую точку, т. с. когда имеет место один из трех случаев, изображенных на рисунке 4.7. Прямые (a, a 3) и (b, b 3) параллельны тогда и только тогда, когда имеет место один из трех случаев, изображенных на рисунке 4.8.
Плоскость может быть задана тремя своими точками, не лежащими на одной прямой, или двумя прямыми (пересекающимися или параллельными), или прямой и точкой, не лежащей на ней. Соответственно каждому из этих способов задания плоскости на плоскости σ должны быть даны аксонометрическая и вторичная проекции элементов, с помощью которых дана плоскость.
Рассмотрим примеры решения простейших задач на взаимное расположение прямых и плоскостей. Эти задачи в дальнейшем будут использованы для построений сечений многогранников.
Задача 1. Прямая (а, а 3) лежит в плоскости, заданной тремя точками (А, A 3), (В, В 3) и (С, С 3), не лежащими на одной прямой. По заданной прямой а построить прямую а 3.
Решение. Найдем сначала точки (М, M 3) и (N, N 3), в которых прямая (a, a 3) пересекает какие-нибудь две из прямых, соединяющих попарно точки (A, A 3), (В, B 3) и (С, С 3). Точки М и N определяются непосредственно из условий задачи (рис. 4.9). Проведя через точки М и N прямые, параллельные оси Oz, строим точки M 3 и N 3, а затем и искомую прямую а 3, которая проходит через эти точки.
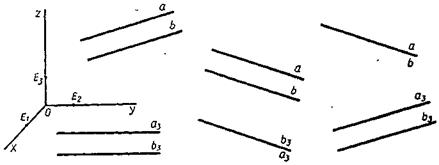
Рис. 4.8
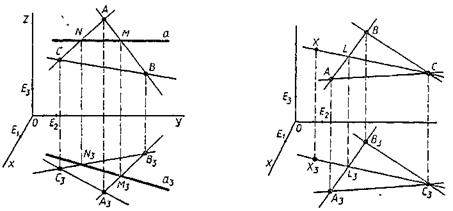
Рис. 4.9
Рис. 40
Замечание. По предположению направление проектирования не параллельно плоскости 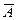
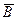
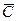 , поэтому точки А, В и С не лежат на одной прямой и, следовательно, предложенный способ решения задачи всегда выполним.
, поэтому точки А, В и С не лежат на одной прямой и, следовательно, предложенный способ решения задачи всегда выполним.
Если точки А 3, В 3 и С 3 лежат на одной прямой р, то в случае пересечения прямых а и Oz, а 3 совпадает с прямой р, в противном случае - а 3 является точкой пересечения прямых а и р.
Задача 2. Точка (X, Х 3) лежит в плоскости, заданной тремя точками (А, А 3), (В, В 3), (С, С 3), не лежащими на одной прямой. По заданной точке Х 3 построить точку X.
Решение. Допустим, что задача решена, т.е. точка X построена (рис. 40). Рассмотрим в пространстве точку 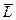 пересечения прямых
пересечения прямых 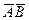 и
и 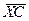 . Очевидно, эта точка лежит в плоскости
. Очевидно, эта точка лежит в плоскости 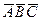 . Ее аксонометрической проекцией является точка L = AB
. Ее аксонометрической проекцией является точка L = AB 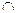 XC, а вторичной проекцией - точка L 3= A 3 В 3
XC, а вторичной проекцией - точка L 3= A 3 В 3 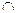 Х 3 С 3. Так как А 3, В 3, C 3 и Х 3 - заданные точки, то легко построить точку L 3, а затем и точку L = AB
Х 3 С 3. Так как А 3, В 3, C 3 и Х 3 - заданные точки, то легко построить точку L 3, а затем и точку L = AB 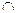 LL 3, где LL 3|| Oz. Проведя прямую LC, строим на ней точку X = LC
LL 3, где LL 3|| Oz. Проведя прямую LC, строим на ней точку X = LC 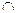 ХХ 3, где XX 3|| Oz.
ХХ 3, где XX 3|| Oz.
4. Пусть прямая 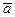 пересекает координатную плоскость
пересекает координатную плоскость 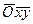 в точке
в точке 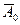 . Аксонометрическая проекция А 0 этой точки называется следом прямой
. Аксонометрическая проекция А 0 этой точки называется следом прямой 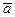 на плоскость
на плоскость 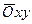 . Легко видеть, что следом данной прямой является точка пересечения аксонометрической и вторичной проекций этой прямой. В самом деле, пусть
. Легко видеть, что следом данной прямой является точка пересечения аксонометрической и вторичной проекций этой прямой. В самом деле, пусть 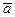 (а, а 3) - данная прямая, а А 0 - точка пересечения прямых а и а 3. Точка
(а, а 3) - данная прямая, а А 0 - точка пересечения прямых а и а 3. Точка 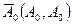 лежит в плоскости
лежит в плоскости 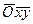 , так как ее аксонометрическая и вторичная проекции совпадают. С другой стороны, А 0
, так как ее аксонометрическая и вторичная проекции совпадают. С другой стороны, А 0 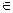 а и А 0
а и А 0 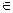 а 3, поэтому
а 3, поэтому 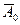 -точка прямой
-точка прямой 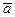 . Таким образом,
. Таким образом, 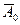 - общая точка плоскости
- общая точка плоскости 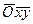 и прямой а, т.е. точка, А 0 - след прямой
и прямой а, т.е. точка, А 0 - след прямой 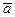 .
.
Список литературы.
1. А. Д. Александров, А. Л. Вернар, В. И. Рыжик, Геометрия М:
 2015-09-06
2015-09-06 847
847








