Полные и неполные изображения. Позиционные задачи

1. Пусть на плоскости σ дано изображение F некоторой фигуры F'. Изображение F называется полным, если к нему можно присоединить изображение R аффинного репера так, что все точки, прямые и плоскости, определяющие фигуру F', будут заданными на плоскости σ. При этом точка M' считается заданной, если на плоскости σ даны ее аксонометрическая проекция М и одна из вторичных проекций, например М ₃. Прямая а' считается заданной, если заданы две ее точки или даны аксонометрическая и одна из ее вторичных проекций. Плоскость считается заданной, если заданы элементы, определяющие ее (три точки, не лежащие на одной прямой, две прямые или следы).

Легко видеть, что изображения многих плоских и пространственных фигур, (плоские n -угольники, призма, пирамида, цилиндр, конус, шар), являются полными. Например, изображение ABCDA'B'C'D' параллелепипеда F ₀ на рисунке 3.5, б является полным. В самом деле, присоединим к нему изображение (А, В, D, А') аффинного репера. Тогда все вершины параллелепипеда F ₀ окажутся заданными, так как для них однозначно определяются аксонометрические и вторичные проекции: (А, А), (В, В), (С, С), (D, D), (А', А), (В', В), (С', С), (D', D). Отсюда следует, что и все ребра и грани параллелепипеда окажутся заданными.

Можно доказать, что свойство изображения быть полным (или неполным) не зависит от выбора присоединенного изображения аффинного репера.

Рассмотрим примеры неполных изображений.

Пример 1. На рисунке 5.1, а изображен шестигранник SABCD. Это изображение не является полным, так как если, например, к нему присоединить изображение (А, В, С, S) аффинного репера, то точки А', B', С' и S' окажутся заданными, а точка D' нет (не определена ее вторичная проекция).

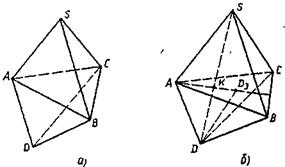
Рис. 5.1

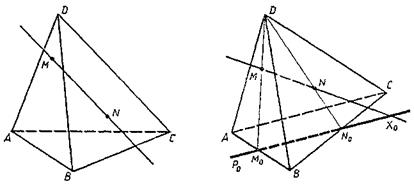
Рис. 5.2

Рис. 5.3

Пример 2. На рисунке 5.2 изображен тетраэдр и прямая. Это изображение не является полным, так как если, например, к нему присоединить изображение (А, В, С, D) репера, то вершины тетраэдра A'B'C'D' окажутся заданными, а точки M' и N' нет (не определены их вторичные проекции).

Число точек, которые надо добавить к чертежу, чтобы неполное изображение сделать полным, называется коэффициентом неполноты данного изображения. В примере 1 коэффициент неполноты равен единице, так как если, например, к рисунку добавить точку К -изображение точки пересечения отрезка S'D' с плоскостью A'B'C' (рис. 5.1, б), то изображение станет полным; теперь вторичную проекцию точки D' легко построить: D ₃ есть точка пересечения прямой АК, с прямой, проведенной через точку D параллельно AS (рис. 5.1, б). В примере 2 коэффициент неполноты равен двум, так как, для того чтобы изображение сделать полным, можно, например, к рисунку 5.2, добавить точки М ₃ и N ₃ - вторичные проекции точек М' и N'.

Можно доказать, что понятие коэффициента неполноты не зависит от выбора присоединенного изображения аффинного репера.

2. Пусть 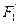и 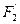две фигуры пространства, а F ₁ и F ₂ - их изображения на плоскости σ, выполненные в одной и той же проекции. Задача построения изображения точек пересечения фигур 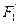и 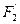называется позиционной задачей. Такие задачи удобно решать, пользуясь методом аксонометрии. Отметим, что любая позиционная задача на полном изображении имеет вполне определенное решение и не содержит никакого произвола. Если же изображение неполное, то, решая позиционную задачу, некоторые элементы можно задать произвольно.

Рассмотрим пример решения позиционной задачи. При решении этой задачи, а также задач следующего параграфа мы не будем отличать точки оригинала (или прямые оригинала) от их аксонометрических проекций; их будем называть просто точками (прямыми). В соответствии с этим точки или прямые оригинала обозначаем теми же буквами (А, В, С,...; а, b, с,...), что и их аксонометрические проекции (а не A', В', С',..; а', b', с',..., как это делалось выше).

Задача. Дано изображение пирамиды DABC и прямой, пересекающей ее грани ABD и BCD в точках М и N (рис. 5.3). Найти след прямой MN на плоскости основания ABC.

Решение. Присоединим к изображению данной пирамиды изображение (А, В, С, D) аффинного репера. Тогда все вершины пирамиды и точки М и N будут заданными, поэтому данное изображение является полным. Прямая MN лежит в плоскости DMN, поэтому след Х ₀ этой прямой лежит на следе р ₀ плоскости DMN, т.е. Х ₀- точка пересечения прямых MN и р ₀. Построим след р ₀ плоскости DMN. Прямые DM и DN пересекают плоскость основания пирамиды в точках M ₀ и N ₀, поэтому прямая р ₀ проходит через точки М ₀ и N ₀, т.е. совпадает с прямой M ₀ N ₀. Таким образом, Х ₀= MN 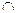M ₀ N ₀.