Изображение плоских фигур в параллельной проекции

Существуют различные способы изображения на плоскости фи­гур, расположенных в пространстве. Здесь следует отметить способ, основанный на параллельном проектировании.

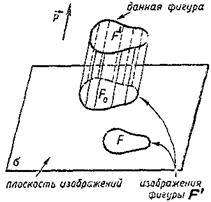
Выберем некоторую плоскость σ и назовем ее плоскостью изображений. Затем возьмем ненулевой вектор 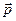, не параллельный плоскости σ. Направление этого вектора назовем направлением проектирования. Пусть F' - произвольная фигура (плоская или пространственная), расположенная в пространстве, a F ₀ - параллельная проекция этой фигуры на плоскость σ. Фигуру F' называют оригиналом, a F ₀ - проекцией оригинала. Любую фигуру F на плоскости σ, подобную фигуре F ₀, называют изображением фигуры F' (рис. 2.1). Построенное таким образом изображение фигуры соответствует ее зрительному восприятию при рассмотрении из точки, расположенной достаточно далеко от фигуры.

Произвол в выборе изображения при данном проектировании (изображением фигуры является не только ее проекция, но и любая фигура, подобная проекции) можно объяснить следующим обстоятельством. Обычно плоскостью изображений служит плоскость листа бумаги и проекция оригинала не всегда помещается на этом листе, а если и помещается, то не всегда удобно расположена. В этих случаях, получив на плоскости σ проекцию F ₀ оригинала F' подвергают плоскость σ преобразованию подобия так, чтобы образ F фигуры F ₀ имел удобное расположение и удобные размеры.

Рис. 2.1

Таким образом, изображение фигуры зависит от выбора плоскости изображений σ, направления проектирования и выбранного подобия плоскости σ. Обычно берется такое изображение фигуры, которое является наиболее наглядным и удобным для выполнения на нем дополнительных построений.

Построение изображений фигур с помощью параллельного проектирования основано на свойствах параллельного проектирования и аффинных отображений. Рассмотрим примеры построений изображений плоских фигур, изучаемых в школьном курсе геометрии. При этом будем считать, что плоскости оригинала и изображения пересекаются и что направление проектирования не параллельно ни одной из этих плоскостей. Для выполнения построений необходимо знать теорему об изображениях плоских фигур.

Рис. 2.2

Теорема. Пусть фигуры F' и, F лежат соответственно на пересекающихся плоскостях σ ' и σ. Фигура F может служить изображением фигуры F' тогда и только тогда, когда фигуры F' и F аффинно-эквивалентны.

1) Пусть фигура F плоскости σ является изображением фигуры F' плоскости σ '. Докажем, что F' и F аффинно-эквивалентны. Рассмотрим проекцию F ₀ фигуры F'. Так как параллельное проектирование является аффинным отображением, то фигура F' аффинно-эквивалентна фигуре F ₀. С другой стороны, F ₀ и F подобны, поэтому они аффинно-эквивалентны. Таким образом, фигуры F' и F аффинно-эквивалентны.

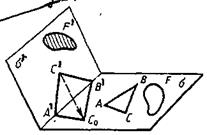
2) Допустим теперь, что фигура F' плоскости σ ' аффинно-эквивалентна фигуре F плоскости σ. Докажем, что фигуру F можно рассматривать как изображение фигуры F'. Так как фигуры F' и F аффинно-эквивалентны, то существует аффинное отображение f: σ ' →σ, такое, что F = f (F'). Выберем репер R' =(А', В', С') плоскости σ ' так, чтобы точки А' и В' лежали на линии пересечения плоскостей σ ' и σ, рассмотрим образ R =(А, В, С) этого репера при отображении f (рис. 2.2).

На плоскости σ построим точку С ₀ так, чтобы ∆ А'В'С ₀ ~ ∆ АВС. Параллельное проектирование f: σ ' →σ по направлению вектора 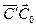репер R' переводит в репер R ₀=(A', В', С ₀). Рассмотрим подобие f ₂: σ→σ, которое репер R ₀ переводит в репер R. Очевидно, f ₂ f ₁: σ→σ является аффинным отображением, которое репер R' переводит в репер R, и поэтому по теореме 1 совпадает с отображением f. Таким образом, F = f ₂ f ₁(F). Но F ₀= f ₁(F') - параллельная проекция фигуры F' на плоскость σ, поэтому F = f ₂(F ₀) - изображение фигуры F'.

Используя предыдущую теорему, рассмотрим построение изображений некоторых многоугольников. По теореме об изображениях плоских фигур изображением n -угольника является фигура, аффинно-эквивалентная оригиналу, т.е. n -угольник. Следовательно, изображением треугольника является треугольник, четырехугольника - четырехугольник, пятиугольника - пятиугольник и т. д. Однако, как следует из той же теоремы, не любой n -угольник плоскости σ может служить изображением данного n -угольника плоскости σ '. Рассмотрим этот вопрос более подробно для n =3 и n =4.

а) Треугольник. Любой треугольник ABC плоскости σ может служить изображением данного треугольника A'В'С' плоскости σ ' если плоскости σ и σ ' пересекаются. В самом деле, по теореме 1 существует аффинное отображение f: σ ' →σ, которое репер (А', В', С') переводит в репер (А, В, С), поэтому треугольники А'В'С' и ABC аффинно-эквивалентны. По предыдущей теореме треугольник ABC может служить изображением треугольника А'В'С'.

б) Четырехугольник. По теореме об изображениях плоских фигур любой четырехугольник плоскости σ, аффинно-эквивалентный данному четырехугольнику F' плоскости σ ' может служить его изображением, если плоскости σ ' и σ пересекаются. Из теоремы 2 заключаем, что не всякий четырехугольник плоскости σ может служить изображением четырехугольника F'. Для построения изображения ABCD данного четырехугольника А'В'С'D' в качестве вершин А, В и С можно выбрать произвольные три точки, не лежащие на одной прямой. При этом изображение D четвертой вершины D' определяется однозначно из условий

(1): (А'С', Е)=(AC, E), (B'D', Е')=(BD, Е), (1)

где Е' и E - точки пересечения прямых А'С', В'D' и AC, BD.

в) Трапеция. Фигурой, аффинно-эквивалентной трапеции, является трапеции, поэтому изображением трапеции является трапеция. Условия (1) в случае трапеции означают, что отношение оснований оригинала равно отношению оснований изображения. Итак, трапеция F -плоскости σ является изображением данной трапеции F' только в том случае, когда отношение оснований трапеции F' равно отношению оснований данной трапеции F'.

г) Параллелограмм (включая ромб, прямоугольник, квадрат) изображается в виде параллелограмма. Так как любые два параллелограмма аффинно-эквивалентны (теорема 2), то любой параллелограмм плоскости изображения является изображением данного параллелограмма - оригинала. В частности, любой параллелограмм плоскости σ является изображением квадрата плоскости σ '.

д) n -Угольник, где n >4. Из предыдущего изложения следует, что для построения изображения данного n -угольника при n >4 три вершины изображения можно выбрать произвольно, а остальные вершины находятся построением.

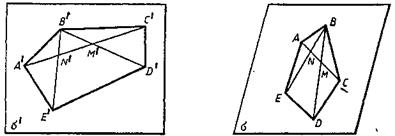
На рисунке 2.3 построено изображение пятиугольника A'B'C'D'E'. Вершины А, В и С выбраны произвольно, а вершины D и Е найдены построением. Вершина D, например, построена с использованием условий (B'D', M')=(BD, M), (A'С', M')=(АС, М). На рисунке 11, построено изображение правильного шестиугольника А'В'C'D'Е'F' с центром в точке О'. В данном случае удобнее брать произвольные точки A, В, О. Точку D строим как точку, симметричную точке A относительно точки О. Для построения точки С строим прямые ВС и DC из условий ВС || АО, DC || BO. Точки Е и F строим как точки, симметричные точкам В и С относительно точки О.

Рис. 2.3

е) Окружность. Построение изображения окружности основано на следующем утверждении.

Лемма. В любом аффинном отображении эллипс (в частности, окружность) переходит в эллипс.

Из этой леммы, учитывая предыдущую теорему, заключаем, что изображением данной окружности является эллипс. При этом изображением центра окружности является центр эллипса, а изображением взаимно перпендикулярных диаметров - сопряженные диаметры эллипса.

Рис. 2.4