Рост населения

Предположим, что население и количество занятых в производстве растут с постоянным темпом прироста n. Тогда изменение капиталовооружённости за год равно Δk= i – dk – nk или Δk= s′f(k) – (d+n)k, где nk – уменьшение капиталовооружённости за счёт распределения капитала между большим количеством работников.

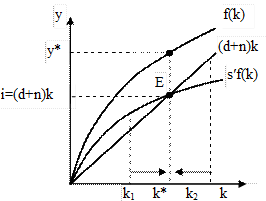
Рис. 10.14 - Устойчивый уровень капиталовооруженности при росте населения

Условие устойчивого долгосрочного равновесия экономики, при неизменной капиталовооружённостиk* выражается равенством s′f(k)=(d+n)k, где (d+ n)k – критическая величина инвестиций, то есть величина, необходимая для поддержания капиталовооружённости на постоянном уровне с учётом амортизации (dk) и инвестиций для обеспечения капиталом новых работников (nk).

В равновесном устойчивом состоянии экономики капиталовооружённость и объём продукции на душу населения остаются неизменными, но поскольку количество населения растёт с темпом n, то капитал и ВВП тоже растут с темпом n.

Если темп прироста населения увеличится с n₁ до n₂, а норма сбережения сохранится на прежнем уровне, то линия (d+n₁)k изменит угол наклона и займёт положение (d+n₂)k.

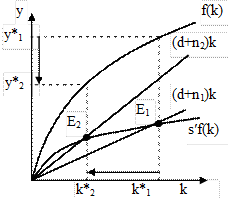
Рис. 10.15 - Падение объемов производства на душу населения при повышении темпов роста населения

Долгосрочное равновесное состояние экономики переместится из точки Е₁ в точку Е₂, уровень капиталовооружённости снизится с k*₁ до k*₂, а производительность труда уменьшится с y*₁ до y*₂.

Итак, в противоположность неокейнсианским моделям модель Р. Солоу обосновывает устойчивость динамического равновесия в длительном периоде в условиях экономического роста, который достигается за счёт роста населения. Однако, если прирост населения не сопровождается соответствующим приростом инвестиций, то будет происходить снижение производительности труда и сокращение ВВП на душу населения.