Есептің қойылымы - бұл кезең есептің мазмұнды қойылымна және шешімнің соңғы мақсатын анықтауға тіреледі.
Математикалық модельді құру - модель физикалық үдерістің негізгі заңдарын дұрыс сипаттауы тиіс. Математикалық модельді құру немесе таңдау математиканың сәйкес бөлімдерін білу және мәселені терең түсінуді талап етеді.
Сандық әдісті жасау- к омпьютер тек қарапайым амалдарды орындайды, ол есептің қойылымын тіпті математикалық тұжырымдаудада түсінбейді. Сандық әдістерді жасаумен есептеу математикасы аумағындағы мамандар айналысады.
Алгоритмді құру- есепті шешу үдерісі аяққы нәтижеге әкелетін және есепті шешу алгоритмі деп аталатын, элементар арифметикалық және логикалық амалдар тізбегі түрінде жазылады. Алгоритмді блок-схема түрінде көрнекті бейнелеуге болады.
Бағдарламалау - есепті шешу алгоритмі машинаға түсінікті тілде амалдардың дәл анықталған тізбегі – компьютерге арналған бағдарлама түрінде жазылады. Бағдарлама құру қандайда бір аралық тіл көмегімен жүргізіледі, ал оны аудару есептеу жүйесінің өзімен жүзеге асырылады.
Бағдарламаны баптау - құрылған бағдарлама әртүрлі қателерден, дәлсіздіктерден, жаңылулардан тұрады. Бағдарламаны машинада баптауға бағдарламаны бақылау, қатені іздеу, оны түзету кіреді.
Есептеулерді жүргізу - бұл кезеңде есептеуге арналған бастапқы деректер дайындалады және бапталған бағдарлама бойынша есептеу жүргізіледі.
Нәтижелерді талдау - есептеу нәтижесі талданады, ғылыми-техникалық құжаттамалар толтырылады.
Қатынастық қателік – бұл абсолюттік қателіктнің санның жуық мәнінәң қатынасына тең.
Есептеу қателігін азайту - а рифметикалық амалдардың нәтижесінде қателікті қарастырғанда жуықтап есептеу салыстырмалы қателіктің көбеюіне алып келеді.
Төзімсіз есеп – дұрыс қойылмаған есеп ретінде қарастырылады. Мұндай есептерге сандық әдіс қолданылмайды.
Дұрыстық- егер берілген тапсырманың кейбір кластар үшін шығыз деректер үшін нақ және жалғыз мәні болса онда тапсырманы корректілі қойылған тапсырма деп атаймыз.
Сандық әдістің жинақтылығы - ол есептің сандық шешімінің нақты шешімге жуықтығын білдіреді
Итерациялық үдерістің жинақтылығы - бұл үдеріс қандайда бір есепті шығару және анықталатын параметрдің ізделіп отырған мәнін табу үшін тізбектеп жуықтау. әдісі құрылады
Әдістің жинақтылығы - деп есептің дискреттік моделінің шешім мәндерінің, дискреттеу парметрлері (мысалы, интегралдау қадамы) нөлге ұмтылған кездегі бастапқы есеп шешімінің сәйкес мәндеріне ұмтылуы түсініледі.
Есептің қойылымы - айталық, y өлшемі x аргументінің функциясы болсын. Бұл дегеніміз, анықтау облысындағы x тің кез келген мәніне сәйкесінше y - тің мәні қойылған.
Теңөлшемді жуықтау - түсінігі үздіксіз жиында - [a,b] кесіндісінде берілген және аппроксимациялайтын функцияларды салыстыруды болжайды. Сондықтан теңөлшемді жуықтау үздіксіз аппроксимациялауға жатады
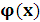 функциясының
функциясының 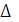 абсолюттік ауытқуы - берілген кесіндідегі олардың арасындағы айырымның абсолюттік шамасының максимал мәніне тең:
абсолюттік ауытқуы - берілген кесіндідегі олардың арасындағы айырымның абсолюттік шамасының максимал мәніне тең:
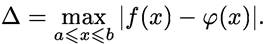
Сызықтық интерполяция- жиі қолданылатын және қарапайым локальды интерполяция түрі. Бұл интерполяцияда берілген нүкте түзу сызықты қиындылармен байланыстырылады 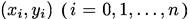 , және f(x) функциясы осы нүктелелерге жақындайды.
, және f(x) функциясы осы нүктелелерге жақындайды.
Квадраттық интерполяция- 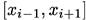 бөлігінде интерполяция функциясы ретінде квадратты үшмүшелік қолданылады.
бөлігінде интерполяция функциясы ретінде квадратты үшмүшелік қолданылады.
Квадраттық үшмүшеліктің теңдеуі:
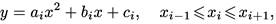 (29)
(29)
Интерполяциялық формуланың қалдық мүшесі- дегеніміз 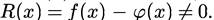 айырымы.
айырымы.
Эмпириялық формула - тәжірибелік деректер негізінде алынған, жуық функционалдық тәуелділік 
Соңғы айырым қатынасы көмегімен туындыны аппроксимациялау (жуықтау)- дегеніміз у' 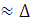 у/
у/ 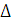 х қатынас
х қатынас
Интегралдық қосынды - 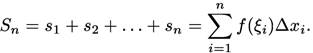
Тікбұрыштар әдісі - сандық интегралдаудың қарапайым әдісі
Формуланың (немесе берілген әдістің) дәлдік реті - берілген квадратуралық формуланың r дәреже көрсеткіші
Дифференциалдық теңдеудің реті- F(x,y,y',...,y(n))=0 кіретін туындының n ең жоғарғы реті
Үлкен туындыға қатысты рұқсат етілген, теңдеу - y' = f(x,y), у" = f(x,y,y').
Сызықтық дифференциал теңдеу - деп, iзделiп отырған функция және оның туындыларына қатысты сызықтық, теңдеуді айтады
Дифференциалдық теңдеуiнiң шешiмi - деп б ар лық n рет дифференциалдалатын у = 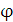 (x) функциясын айтады
(x) функциясын айтады
Коши теоремасы - егер (2) теңдеуінің оң бөлігі f(x,y) және оның жеке туындысы 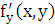 анықталған және
анықталған және 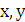 айнымалыларының өзгеру G қандайда бір аумағында үздіксіз болса, онда осы аумақтың барлық (x0, у0) ішкі нүктелері үшін берілген теңдеу х = х0 болғанда у = у0 берілген мәнін қабылдайтын, жалғыз шешімге ие болады.
айнымалыларының өзгеру G қандайда бір аумағында үздіксіз болса, онда осы аумақтың барлық (x0, у0) ішкі нүктелері үшін берілген теңдеу х = х0 болғанда у = у0 берілген мәнін қабылдайтын, жалғыз шешімге ие болады.
Эйлер әдісі - қарапайым дифференциалды теңдік үшін Коши есебін шешудің ең қарапайым сандық әдісі Эйлер әдісі болып табылады.
Гиперболалық теңдеу:
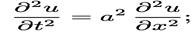
Жылуөткiзу немесе диффузия теңдеуi (параболалық)
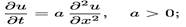
Лаплас теңдеуі (эллиптикалық)
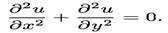
Бiрқалыпты тор - барлық ұяшықтарда торлар бiрдей болу керек
Дәріс конспектісі
Дәріс №1. Тақырыбы: КІРІСПЕ.
Сабақ жоспары:
- Кіріспе
- Компьютерде есепті шешу кезеңдері.
 2015-09-06
2015-09-06 900
900








