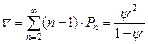 ,
,
проще
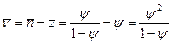 .
.
Пример 1.1.
В магазин приходят покупатели в среднем каждые две минуты. Работает один продавец, который обслуживает покупателя в среднем 2.5 минуты. Время прихода и обслуживания подчиняется экспоненциальному закону.
Определить:
- вероятность простоя продавца 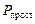 ;
;
- вероятность занятости продавца 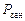 ;
;
- ероятность того, что в очереди ровно два покупателя 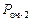 ;
;
- вероятность наличия очереди в магазине 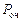 .
.
Определим сначала интенсивности входного потока и обслуживания
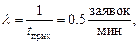
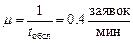 .
.
При данных характеристиках система не имеет стационарного режима (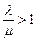 ) и дальнейшие расчеты не имеют смысла.
) и дальнейшие расчеты не имеют смысла.
Пусть новый продавец обслуживает покупателей в среднем 1.2 мин. Тогда 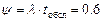 — система стационарна.
— система стационарна.
Продавец простаивает, если в магазине нет ни одного покупателя и 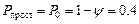 . Продавец занят, если в магазине есть хотя бы один покупатель, тогда
. Продавец занят, если в магазине есть хотя бы один покупатель, тогда 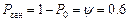 .
.
В очереди будет находиться ровно две заявки, если в магазине будет находиться три покупателя (два в очереди, один на обслуживании) и 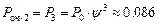 .
.
Очередь образуется, если покупателей больше одного: 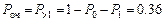 .
.
1.6 Схема гибели и размножения
После преобразований уравнений Колмогорова очевидно, что вероятности того, что система не изменит свое состояние 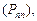 не влияют на вероятности состояний (образуют в уравнениях пару слагаемых с противоположными знаками). Поэтому в дальнейшем на графах переходов мы будем указывать только вероятности переходов типа
не влияют на вероятности состояний (образуют в уравнениях пару слагаемых с противоположными знаками). Поэтому в дальнейшем на графах переходов мы будем указывать только вероятности переходов типа 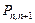 и
и  и указывать только интенсивности переходов. Тогда в общем случае для марковских систем мы получаем граф переходов следующего вида:
и указывать только интенсивности переходов. Тогда в общем случае для марковских систем мы получаем граф переходов следующего вида:
Рисунок 1.3 – Граф переходов
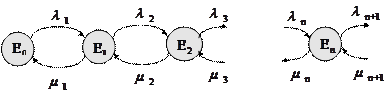 |
 Здесь каждое из средних состояний связано прямой и обратной стрелкой с каждым из соседних состояний. Такой граф называется схемой гибели и размножения. Найдем один раз и навсегда для этой схемы вероятности состояний установившегося режима.
Здесь каждое из средних состояний связано прямой и обратной стрелкой с каждым из соседних состояний. Такой граф называется схемой гибели и размножения. Найдем один раз и навсегда для этой схемы вероятности состояний установившегося режима.
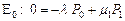 или
или 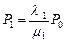 ,
,
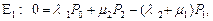 отсюда
отсюда 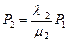 ,
,
аналогично
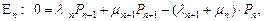 отсюда,
отсюда, 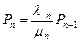 .
.
Преобразуем
 ,
,
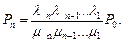
Учитывая, что 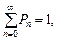 получаем
получаем
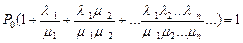
и
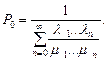
Полученные формулы мы будем в дальнейшем использовать для расчета вероятностей состояний различных СМО.
1.7 Формула Литтла
Выведем еще одну важную формулу, связывающую (для стационарного режима) среднее число заявок 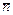 в системе и среднее время пребывания заявки
в системе и среднее время пребывания заявки 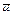 в системе.
в системе.
Для любой СМО, если в системе установился стационарный режим, среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность 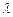 .
.
Обозначим 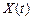 — число заявок, прибывших в СМО до момента
— число заявок, прибывших в СМО до момента 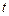 ;
; 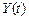 —число заявок, покинувших СМО до момента
—число заявок, покинувших СМО до момента 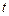 . Обе функции случайны и меняются скачком (на 1) в моменты прихода и ухода заявок. Примерный вид функций приведен на рисунке 1.4.
. Обе функции случайны и меняются скачком (на 1) в моменты прихода и ухода заявок. Примерный вид функций приведен на рисунке 1.4.
 |
Рисунок 1.4 - Функции X(t),Y(t)
Очевидно, что для любого момента 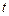 :
: 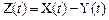 — число заявок, находящихся в СМО.
— число заявок, находящихся в СМО.
Рассмотрим большой интервал времени 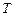 и вычислим для него среднее число заявок, находящихся в СМО.
и вычислим для него среднее число заявок, находящихся в СМО.
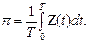
Этот интеграл — площадь заштрихованной фигуры, которая состоит из прямоугольников в 1 высотой и с основанием, равным времени пребывания в системе соответствующей заявки 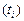 .
.
Тогда 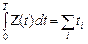 и
и 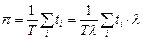 ,
,
где  - это среднее число заявок, пришедших за время
- это среднее число заявок, пришедших за время 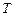 . Если разделить сумму всех времен
. Если разделить сумму всех времен 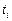 на среднее число заявок, то получим среднее время пребывания заявки в системе
на среднее число заявок, то получим среднее время пребывания заявки в системе 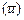 :
: 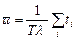 , тогда
, тогда 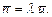 Откуда получаем формулу Литтла
Откуда получаем формулу Литтла
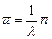 .
.
Для любой СМО среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Аналогично выводится формула, связывающая среднее число заявок в очереди (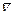 ) и среднее время пребывания заявки в очереди (
) и среднее время пребывания заявки в очереди (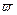 ):
):  .
.
1.8 Одноканальная СМО с отказами
Простейшая задача: СМО содержит один канал обслуживания; заявка, поступившая на вход системы и заставшая канал занятым, получает отказ. Граф переходов:
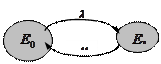 |

Рисунок 1.5 – Граф переходов
Тогда 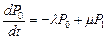 ,
, 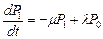 .
.
Исходя из условия 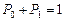 и начальных условий
и начальных условий 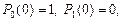 получаем
получаем
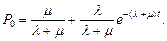
Для стационарного режима 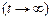
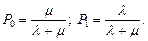
Получим некоторые характеристики СМО.
Вероятность отказа: заявка получит отказ, если канал занят
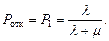
Относительная пропускная способность (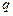 )равна среднему числу обслуженных заявок к общему числу поступивших заявок (показывает долю обслуженных заявок)
)равна среднему числу обслуженных заявок к общему числу поступивших заявок (показывает долю обслуженных заявок) 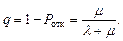
Абсолютная пропускная способность (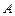 ) —число обслуженных заявок в единицу времени —
) —число обслуженных заявок в единицу времени — 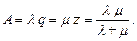
Среднее число занятых каналов (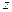 )равно среднему числу заявок в системе —
)равно среднему числу заявок в системе — 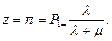
Среднее время, проведенное заявкой в системе 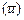
 2015-10-14
2015-10-14 406
406








