Имеется одна телефонная линия, по которой звонки поступают с интенсивностью в среднем 0.8 зв/мин. Среднее время телефонного разговора равно 1.5 мин. Если линия занята, то звонок получает отказ. Необходимо определить:
- вероятность отказа 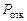 ;
;
- абсолютную пропускную способность 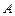 ;
;
- среднее количество занятых каналов 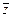 .
.
Так как СМО с отказами, то стационарный режим существует всегда.
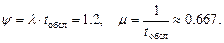
Заявка получает отказ, если линия занята, и 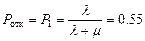 , (т.е. в среднем только 45% звонков получают обслуживание).
, (т.е. в среднем только 45% звонков получают обслуживание).
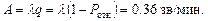
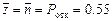 — телефонная линия занята в среднем всего лишь 55% от общего времени.
— телефонная линия занята в среднем всего лишь 55% от общего времени.
1.9 Одноканальная СМО с ограниченной очередью
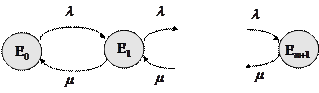 Пусть длина очереди в одноканальной СМО ограничена числом
Пусть длина очереди в одноканальной СМО ограничена числом 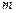
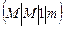 . Тогда граф переходов будет иметь следующий вид:
. Тогда граф переходов будет иметь следующий вид:
Рисунок 1.6– Граф переходов
Используя формулы схемы гибели и размножения, получаем
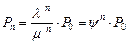 ,
, 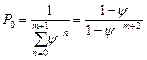 .
.
Среднее число занятых каналов 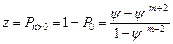 .
.
Среднее число заявок в очереди
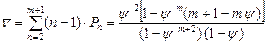 .
.
Среднее число заявок в системе 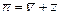 .
.
Вероятность в отказе 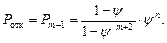
Относительная пропускная способность
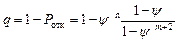 .
.
1.10 Многоканальные СМО с ожиданием
Рассмотрим случай 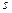 одинаковых каналов обслуживания
одинаковых каналов обслуживания 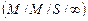 с интенсивностью обслуживания
с интенсивностью обслуживания 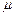 каждого прибора. При простейшем входном потоке и экспоненциальном времени обслуживания правило выбора канала не влияет на функционирование системы, т.е. на число заявок, находящихся в системе, на время ожидания.
каждого прибора. При простейшем входном потоке и экспоненциальном времени обслуживания правило выбора канала не влияет на функционирование системы, т.е. на число заявок, находящихся в системе, на время ожидания.
Построим граф переходов
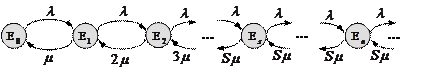 |
Рисунок 1.7 – Граф переходов
Интенсивность обслуживания возрастает с ростом числа занятых каналов. Как только все каналы оказываются занятыми заявками, интенсивность обслуживания в системе перестает расти, вновь пришедшие заявки становятся в очередь, ожидая освобождения какого-либо из каналов.
По графу строим уравнения вероятностей состояний
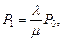
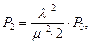
....
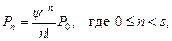
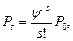
....
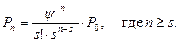
Учитывая 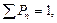
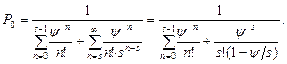
Получим основные характеристики системы
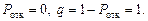
Абсолютная пропускная способность
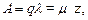
отсюда, среднее число занятых каналов
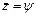 .
.
Среднее число заявок в очереди
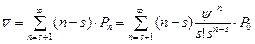 ,
,
после преобразований 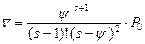 .
.
Общее число заявок в системе: 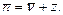
Среднее время пребывания в системе
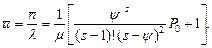
Все вышеперечисленные формулы справедливы только для стационарного режима. Для того, чтобы многоканальная система с бесконечной очередью имела стационарный режим, должно выполняться условие 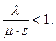
1.11 Многоканальные СМО с отказами
Имеется 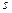 обслуживающих каналов, каждый из которых доступен, когда он свободен, для каждой из поступающих в систему заявок. Если при поступлении очередной заявки все каналы заняты, то заявка получает отказ и теряется (
обслуживающих каналов, каждый из которых доступен, когда он свободен, для каждой из поступающих в систему заявок. Если при поступлении очередной заявки все каналы заняты, то заявка получает отказ и теряется (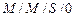 ). Граф переходов
). Граф переходов
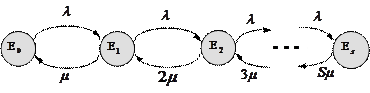 |
Рисунок 1.8 – Граф переходов
Уравнения вероятностей состояний здесь такие же, как и для любой многоканальной СМО, только для условия 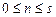
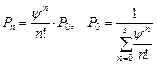 .
.
Заявка получает отказ в том случае, если все каналы заняты, тогда вероятность отказа
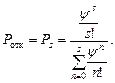
Относительная пропускная способность
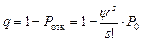 .
.
Учитывая, что 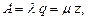 среднее число занятых каналов равно
среднее число занятых каналов равно
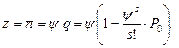
Среднее время, проводимое заявкой в системе
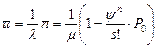
Если в системе очередь, ограниченная числом мест 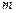 (M / M / s / m), то заявка получит отказ только в том случае, когда в системе заняты все каналы обслуживания и все места в очереди (
(M / M / s / m), то заявка получит отказ только в том случае, когда в системе заняты все каналы обслуживания и все места в очереди (
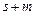 заявок). Тогда вероятность отказа
заявок). Тогда вероятность отказа
 где
где 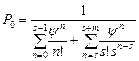 .
.
Абсолютная пропускная способность
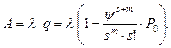
Формулы для среднего числа заявок в системе, в очереди и на обслуживании аналогичны соответствующим формулам для многоканальной СМО с ожиданием.
 2015-10-14
2015-10-14 635
635








