Определение скорости полета снаряда с помощью баллистического крутильного маятника
ЗАКОН ИЗМЕНЕНИЯ МОМЕНТА ИМПУЛЬСА И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Моментом импульса материальной точки относительно некото-рого центра О называется векторное произведение 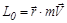 , где
, где 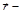 радиус-вектор материальной точки, проведенный из центра О
радиус-вектор материальной точки, проведенный из центра О
(рис. 5.1), 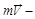 импульс материальной точки. Величина момента импульса равна
импульс материальной точки. Величина момента импульса равна 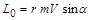 , где α – угол между векторами
, где α – угол между векторами 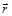 и
и 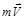 .
.
Проекция вектора 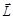 , на ось Z, проходящую через точку 0, называется моментом импульса материальной точки относительно этой оси
, на ось Z, проходящую через точку 0, называется моментом импульса материальной точки относительно этой оси
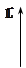 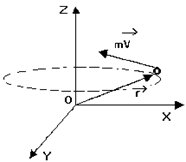 Рис. 5.1 Рис. 5.1 |
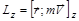 . Если скорость точки лежит в плоскости, перпендикулярной оси Z, то
. Если скорость точки лежит в плоскости, перпендикулярной оси Z, то 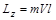 , где
, где 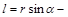 кратчайшее расстояние от оси вращения до прямой, вдоль которой направлена скорость.
кратчайшее расстояние от оси вращения до прямой, вдоль которой направлена скорость.
Для твердого тела, вращавшегося вокруг неподвижной оси, момент импульса определяется выражением 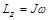 , где
, где
J – момент инерции тела относительно оси вращения, ω – угловая скорость вращения.
Момент импульса системы тел определяется выражением
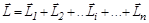 , (5.1)
, (5.1)
где 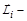 момент импульса i -го тела. Известно, что производная по времени от момента импульса механической системы равна моменту внешних сил, действующих на эту систему:
момент импульса i -го тела. Известно, что производная по времени от момента импульса механической системы равна моменту внешних сил, действующих на эту систему:
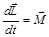 , (5.2)
, (5.2)
где 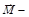 момент внешних сил. Это утверждение в механике называют законом изменения момента импульса (II законом Ньютона для вращательного движения). Если система замкнутая, то
момент внешних сил. Это утверждение в механике называют законом изменения момента импульса (II законом Ньютона для вращательного движения). Если система замкнутая, то 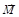 равен нулю, и момент импульса системы остается постоянным. Это утверждение называют законом сохранения момента импульса.
равен нулю, и момент импульса системы остается постоянным. Это утверждение называют законом сохранения момента импульса.
Закон сохранения момента импульса относительно некоторой оси формулируется следующим образом: если момент внешних сил, действующих на систему относительно некоторой оси равен нулю, то момент импульса системы по отношению к той же оси остается постоянным.
 2015-10-16
2015-10-16 2517
2517