Результирующая всех сил действ.на СМТ определ. следующим образом 
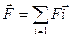 (1).
(1).
Где 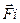 -результирующая всех сил как со стороны внешних сил так и стороны других тел
-результирующая всех сил как со стороны внешних сил так и стороны других тел 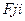 .
.
Разумное предположение что 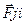 =0 на себя не действует,тогда получим следующее равенство
=0 на себя не действует,тогда получим следующее равенство 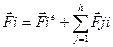 (2)
(2)
Учтем что между точками системы действуют системы которые подчиняются 3 закону Ньютона преобразуем ф(1)
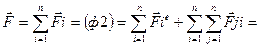


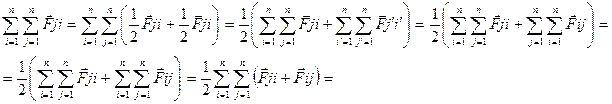
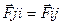 (3)
(3)
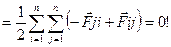
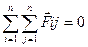
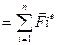
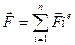 (4)
(4)
Результирующая сила действующая на СМТ=сумме действующ.внешних сил.
Результирующим моментом сил, действующ.на СМТ назовем вектор 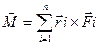 (5)
(5) 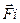 -дается ф(2)
-дается ф(2)
Преобразуем 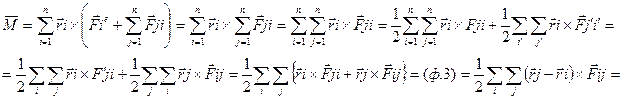
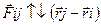 (6)
(6)
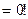
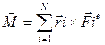 (7)
(7)
Результирующий момент сил действующ.на СМТ =сумме моментов внешних сил.
12.Уравнение движения для СМТ.
1.Урав-е для импульса СМТ
2.Урав-е для момента импульса СМТ
В основе вывода лежит определение 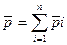 (1) импульса СМТ.Это справедливо для
(1) импульса СМТ.Это справедливо для 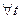 .Дифференцируем обе части
.Дифференцируем обе части 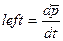
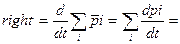
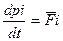 (2)
(2)
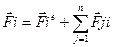 (3)
(3)
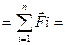
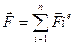 (4)
(4)
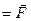 приравнивая л.и пр.части окончательно получаем:
приравнивая л.и пр.части окончательно получаем: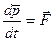 (5)
(5)
Полученное ур-е(5) называется ур-ем движения для импульса СМТ. p-суммарный импульс системы (1).F-результирующая сил действ.на СМТ(4).
2.Вывод ур-я движения для момента импульса СМТ. Рассмстрим одну частицу введем систему отсчета.В лекции №6 мы вывели ур-е движения для одной МТ.Воспользуемся результатами прошлой лекции.Логика такая же как и при выводе ур-я для импульса.
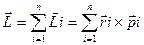 (6)
(6)
работает для 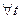 . Продифференцируем по t.
. Продифференцируем по t.
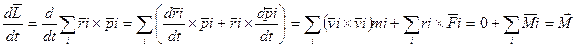

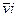 -скорость частицы
-скорость частицы
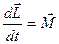 (7) работает для всех МТ.
(7) работает для всех МТ.
Ур-е (7) есть искомое ур-е движения для момента импульса СМТ.L-момент количества движения СМТ(6).М-момент сил действ. на СМТ.(см.прошлую лекцию ф №7)
13.Уравнение для момента импульса СМТ.
Вывод ур-я движения для момента импульса СМТ. Рассмстрим одну частицу введем систему отсчета.В лекции №6 мы вывели ур-е движения для одной МТ.Воспользуемся результатами прошлой лекции.Логика такая же как и при выводе ур-я для импульса.
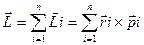 (6)
(6)
работает для 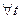 . Продифференцируем по t.
. Продифференцируем по t.
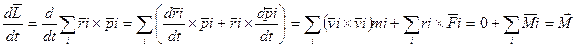

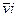 -скорость частицы
-скорость частицы
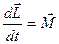 (7) работает для всех МТ.
(7) работает для всех МТ.
Ур-е (7) есть искомое ур-е движения для момента импульса СМТ.L-момент количества движения СМТ(6).М-момент сил действ. на СМТ.(см.прошлую лекцию ф №7)
 2014-02-02
2014-02-02 1593
1593








