Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
- Максимальное значение -
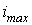 .
. - Действующее значение -
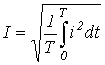 .
. - Среднее по модулю значение -
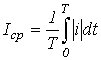 .
. - Среднее за период значение (постоянная составляющая) -
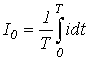 .
. - Коэффициент амплитуды (отношение максимального значения к действующему) -
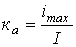 .
. - Коэффициент формы (отношение действующего значения к среднему по модулю) -
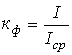 .
. - Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) -
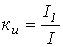 .
. - Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) -
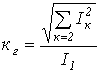 .
.
Разложение периодических несинусоидальных
кривых в ряд Фурье
Из математики известно, что всякая периодическая функция 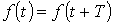 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
, где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
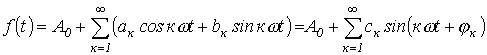 . .
| (1) |
Здесь 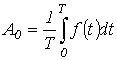 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника; 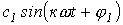 - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой 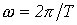 , где Т – период несинусоидальной периодической функции.
, где Т – период несинусоидальной периодической функции.
В выражении (1) 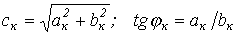 , где коэффициенты
, где коэффициенты 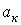 и
и 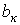 определяются по формулам
определяются по формулам
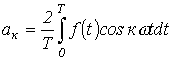 ;
;
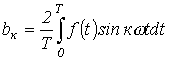 .
.
 2015-10-16
2015-10-16 244
244








