2015-10-16
590
Содержание
1. Цель работы……………………………………………………………4
2. Теоретическая часть…………………………………………………..4
3. Экспериментальная часть…………………………………………….6
3.1. Описание установки…………………………………………………8
3.2. Требования по технике безопасности……………………………...9
3.3. Порядок выполнения работы……………………………………...10
4. Контрольные вопросы………………………………………………..11
Список литературы……………………………………………………..11
ЛАБОРАТОРНАЯ РАБОТА № 14
НАКЛОННЫЙ МАЯТНИК
Цель работы
1.1. Изучение силы трения качения.
1.2. Определение коэффициента трения качения.
Теоретическая часть
Рассмотрим движение шара массой m и моментом инерции Jc по горизонтальной поверхности под действием силы F (x), приложенной к центру масс С, причем предположим, что тело и поверхность абсолютно жесткие, т.е. тело не деформируется, а касается поверхности в одной точке О (рис. 2.1.).
 |
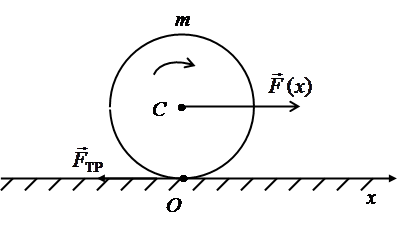Рис. 2.1.
Со стороны поверхности на тело действует сила трения F ТР. Точки шара участвуют в двух видах движения: центр масс С движется поступательно вдоль оси х, точки поверхности шара вращаются вокруг горизонтальной оси, проходящей через центр масс.
|
|
|
Уравнение движения шара на основе законов поступательного и вращательного движения имеют вид:
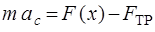, (2.1)
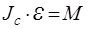, (2.2)
где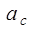 
– ускорение центра масс; 
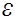– угловое ускорение шара; М – момент сил, действующих на тело, относительно оси, проходящей через центр масс; 
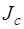– момент инерции шара относительно оси, проходящей через точку С. Момент силы F относительно точки С равен нулю, следовательно:
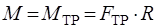. (2.3)
По определению,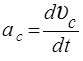 
, 
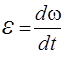, где ω–угловая скорость; υс – линейная скорость центра масс.
Предположим, что шар движется по поверхности со слабым проскальзыванием. В этом случае скорость точки касания (точки О на рис. 2.1), являющейся скоростью проскальзывания, будет равна
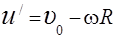, (2.4)
причем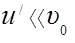 
.
Тело скользит по поверхности со скоростью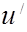 
, на него действует сила трения, совершающая отрицательную работу, вследствие чего полная механическая энергия системы уменьшается, т.е.
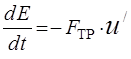, (2.5)
где Е полная механическая энергия равная
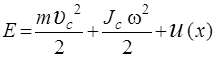. (2.6)
Продифференцировав последнее соотношение и учитывая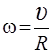, что 
и что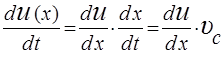 
, получим
.
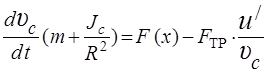Оно аналогично уравнению движения материальных точек
,
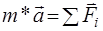m * – масса, равная
,
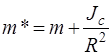а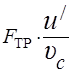 
– сила трения качения:
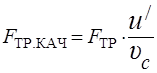. (2.7)
На практике часто реализуется случай, когда сила трения качения не зависит от скорости тела. В этом случае скорость проскальзывания 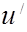пропорциональна скорости тела, т.е.
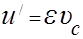и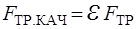 
. (2.8)
Обычно коэффициент пропорциональности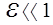 
.
Сила трения скольжения определяется силой нормальной реакции опоры N и коэффициентом трения скольжения μ:
|
|
|
.
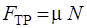Учитывая (2.8), получим для силы трения качения
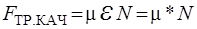, (2.9)
где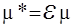 
– коэффициент трения качения.
