Теория метода и описание установки

Момент инерции тел правильной формы может быть вычислен теоретически. Если же тело имеет сложную форму (рис. 6), то теоретически определять его момент инерции трудно. Одним из методов экспериментального определения момента инерции тела является метод крутильных колебаний.

Используемый в данной работе крутильный маятник представляет собой металлическую рамку с приспособлениями для удержания исследуемых тел в горизонтальном положении, подвешенную на упругой нити (см. рис. 7, 8). На рамке закреплены два съёмных груза m₁, что позволяет изменять момент инерции колебательной системы (см. рис. 8, 9).

Рис. 6. Твёрдые тела, моменты инерции которых нужно определить (металлические параллелепипеды и куб).

Рис. 7. Приспособление для удержания исследуемых тел в горизонтальном положении.

Рис. 8. Внешний вид установки для измерения моментов инерции различных твёрдых тел методом крутильным колебаний.

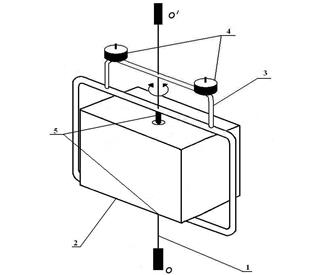
Рис. 9. Схематическое устройство крутильного маятника с исследуемым телом.

1 – упругая нить

2 – исследуемое тело

3 – рамка

4 – съёмные грузы (m₁)

5 – держатели исследуемого тела

6 – d – расстояние от центров масс грузов до оси ОО’ (d = 0,0525 м)

7 – r – радиус грузов (r = 0,015м).

При отклонении рамки на небольшой угол система начинает совершать колебательные движения в горизонтальной плоскости вокруг вертикальной оси OO’ (рис. 9). При вращении рамки в нити возникают упругие силы, которые стремятся вернуть рамку в положение равновесия.

Уравнение колебаний может быть получено с помощью основного уравнения динамики вращательного движения твёрдого тела:

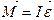где М - момент сил упругости, ε – угловое ускорение маятника с грузами m₁. В свою очередь M = – D α. Знак (-) указывает на то, что этот момент возвращает систему в состояние устойчивого положения равновесия. Тогда

I₁ε = –D α, (1)

где α – угол поворота рамки с закрепленным на нём исследуемым телом; D -модуль кручения; I₁ –моментинерциимаятника сгрузами m₁.

Учитывая, что угловое ускорение ε = 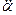, перепишем уравнение (1) в виде

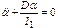Введя обозначение 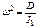, приходим к уравнению

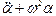= 0.

А это - дифференциальное уравнение гармонических колебаний и его решением является уравнение вида: α = α ₀sin ωt. Поскольку период колебаний 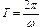, то формула для определения периода колебаний крутильного маятника с грузами m ₁ запишется в виде:

T ₁ = 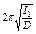, (2) откуда 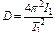. (2а)

Уменьшим момент инерции системы на величину ∆I, сняв оба груза m₁. Согласно теореме Штейнера, можно найти изменение момента инерции системы ∆I = 2(I_с + m₁d²), где I_с = 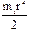– момент инерции грузов - дисков (массой m₁и радиуса r) относительно собственной оси симметрии, через d обозначено расстояние от оси ОО^' до оси грузов. Значение нового периода колебаний системы Т для системы со снятыми грузами m ₁:

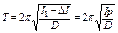, (3) откуда 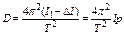. (3а)

Совместное рассмотрение (2а) и (3а) позволяет получить значение для момента инерции I _р(момента инерции пустой рамки).

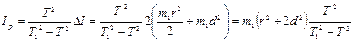. (4)

Если снять грузы m ₁и установить в рамке исследуемый образец согласно (рис. 7), то проведя аналогичные приведённым выше рассуждениям, его момент инерции можно записать

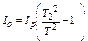, (5)