 При вращении твердого тела вокруг неподвижной оси отдельные точки тела описывают окружности, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R и за бесконечно малый промежуток времени dt совершает поворот на угол
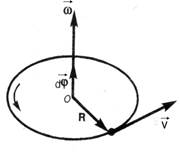
При вращении твердого тела вокруг неподвижной оси отдельные точки тела описывают окружности, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R и за бесконечно малый промежуток времени dt совершает поворот на угол 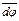 (малый поворот рассматривается как вектор, модуль которого равен углу поворота dφ, а направление подчиняется правилу правого винта (рис. 1)).
(малый поворот рассматривается как вектор, модуль которого равен углу поворота dφ, а направление подчиняется правилу правого винта (рис. 1)).
Угловой скоростью 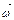 называется векторная физическая величина, определяемая первой производной угла поворота по времени:
называется векторная физическая величина, определяемая первой производной угла поворота по времени:
|
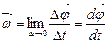 .
. Вектор 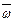 , как и вектор
, как и вектор 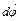 , направлен вдоль оси вращения по правилу правого винта (рис. 1).
, направлен вдоль оси вращения по правилу правого винта (рис. 1).
Угловым ускорением 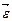 называется векторная физическая величина, определяемая первой производной угловой скорости по времени:
называется векторная физическая величина, определяемая первой производной угловой скорости по времени:
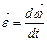 .
.
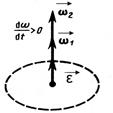
При ускоренном движении вектор 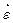 по направлению совпадает с
по направлению совпадает с 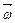 (рис.2, а), а при замедленном -
(рис.2, а), а при замедленном - 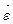 и
и 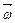 направлены противоположно друг другу (рис. 2,б).
направлены противоположно друг другу (рис. 2,б).
 а а | 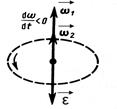 б б |
Рис. 2
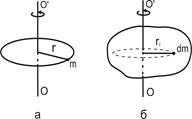 Моментом инерции I материальной точки называется скалярная физическая величина, определяемая произведением ее массы m на квадрат радиуса окружности r, по которой она может двигаться относительно некоторой произвольно выбранной оси ОО' (рис. 3,а).
Моментом инерции I материальной точки называется скалярная физическая величина, определяемая произведением ее массы m на квадрат радиуса окружности r, по которой она может двигаться относительно некоторой произвольно выбранной оси ОО' (рис. 3,а).
|
просуммировать моменты инерции этих, так называемых, элементарных масс, то получим
момент инерции всего тела
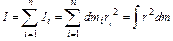 ,
,
где ri – радиус вращения i – той элементарной массы, а интеграл берется по всему объему тела (рис. 3,б). Для однородных тел, для которых плотность 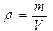 (где m – масса тела, а V – его объем, т.е. плотность определяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле
(где m – масса тела, а V – его объем, т.е. плотность определяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле
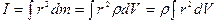 .
.
Теорема Штейнера
Если известен момент инерции тела относительно оси ОО', проходящей через центр масс тела (обозначим его Io), то момент инерции тела относительно любой параллельной ей оси ZZ'
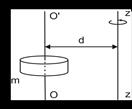 (обозначим его I) равен
(обозначим его I) равен
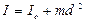 ,
,
где m – масса тела, d – расстояние между осями (рис. 4).
|
|
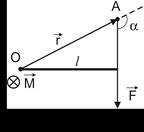
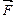 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора
относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора 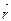 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу 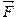 (рис. 5):
(рис. 5): 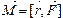 .
. Модуль момента силы равен 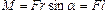 , где α – угол между
, где α – угол между 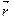 и
и 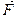 ,
, 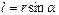 - плечо силы
- плечо силы 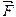 (l - длина перпендикуляра, опущенного из точки О на направление действия силы (рис. 5)).
(l - длина перпендикуляра, опущенного из точки О на направление действия силы (рис. 5)).
 Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси: 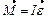 , то есть направление
, то есть направление 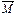 совпадает с направлением
совпадает с направлением 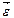 (рис. 4). Моментом силы Mz относительно неподвижной оси ZZ' называется проекция этого момента на данную ось.
(рис. 4). Моментом силы Mz относительно неподвижной оси ZZ' называется проекция этого момента на данную ось.
|
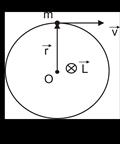
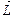 материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора
материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора 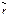 этой материальной точки, проведенного из точки О, на величину ее импульса
этой материальной точки, проведенного из точки О, на величину ее импульса 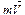 (m - масса материальной точки,
(m - масса материальной точки, 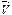 – ее скорость при поступательном движении или линейная скорость ее при вращательном движении), то есть
– ее скорость при поступательном движении или линейная скорость ее при вращательном движении), то есть 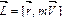 . Вектор
. Вектор 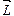 направлен так же, как и вектор угловой скорости
направлен так же, как и вектор угловой скорости 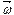 , т. е. вдоль оси вращения, согласно правилу правого винта (рис. 6).
, т. е. вдоль оси вращения, согласно правилу правого винта (рис. 6). Если твердое тело, вращающееся вокруг некоторой неподвижной оси ZZ', представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела Lz относительно этой оси. Суммирование производим по всем элементарным массам mi, на которые разбивается тело.
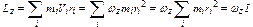 ,
,
так как 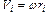 , где ω - угловая скорость вращения тела, I – момент инерции твердого тела. В общем случае
, где ω - угловая скорость вращения тела, I – момент инерции твердого тела. В общем случае 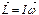 .
.
Закон сохранения момента импульса: момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.
Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки. Кинетическая энергия материальной точки массы m при поступательном движении со скоростью V определяется фор-мулой Ек = 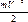 . При вращательном движении роль массы m выпол-няет момент инерции I, а вместо скорости V выступает угловая скорость ω, и формула кинетической энергии при вращательном движении материальной точки приобретает вид: Eк вращ
. При вращательном движении роль массы m выпол-няет момент инерции I, а вместо скорости V выступает угловая скорость ω, и формула кинетической энергии при вращательном движении материальной точки приобретает вид: Eк вращ 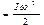 .
.
Потенциальная энергия измеряется работой, которую тело может совершить при перемещении его из одного простран-ственного положения в другое. Так, потенциальная энергия тела массы m, поднятого на высоту h над поверхностью Земли Eпот = mgh. Потенциальная энергия упруго деформированной пружины Епот = 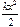 , где k – коэффициент упругости, х – деформация пружины. Потенциаль-ная энергия при закручивании стержня Епот =
, где k – коэффициент упругости, х – деформация пружины. Потенциаль-ная энергия при закручивании стержня Епот = 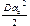 , где D – константа, зависящая от упругих свойств стержня при его кручении (так называ-мый модуль кручения), αо – угол деформации при закручивании.
, где D – константа, зависящая от упругих свойств стержня при его кручении (так называ-мый модуль кручения), αо – угол деформации при закручивании.
Закон сохранения механической энергии гласит: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной, возможны лишь превращения кинетической энергии в потенциальную и наоборот. Напомним, что консервативными называют силы, работа которых по замкнутой траектории равна нулю. Так, при закручивании упругого стержня (нити) закон сохранения энергии может быть записан как 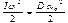 .
.
 2015-10-16
2015-10-16 1231
1231
