2015-10-16
214
Фізичним маятником називається тверде тіло, яке може коливатись відносно нерухомої точки, яка не збігається з його центром мас, під дією сили тяжіння.
У положенні рівноваги центр мас маятника розміщується на вертикалі, яка проходить через центр мас. При відхиленні маятника від положення рівноваги на деякий кут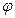 
(рис.13.1) виникає момент сили, який намагається повернути маятник у положення рівноваги. У випадку малих значень кута 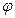, коли можна вважати, що 
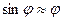, цей момент (рис.13.1)
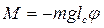, (13.1)
де m – маса маятника;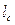 
– відстань від осі до центра мас.
Знак «–» в (13.1) означає, що момент М спрямований протилежно кутовому зміщенню .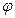
Позначимо момент інерції маятника відносно точки підвісу (осі коливання) І та візьмемо до уваги, що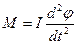 
. Тоді (113.1) набуде вигляду
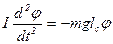, (13.2)
або
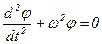, (13.3)
де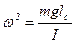 
. (13.4)
Розв’язавши диференціальне рівняння (13.3), дістанемо рівняння коливального руху маятника
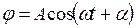, (13.5)
де А – амплітуда коливань маятника (найбільше відхилення маятника від положення рівноваги);
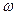– циклічна частота; t – час; 
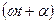– фаза коливання; 
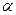– початкова фаза
(при t =0).
Час, за який фізичний маятник здійснює повне коливання, називається періодом коливань Т.
Циклічна частота пов’язана з періодом коливань співвідношенням
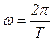, (13.6)
З цього випливає, що циклічна частота – це число коливань за 2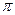 
секунд. Період коливання фізичного маятника 
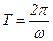, або з урахуванням (13.4)
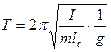. (13.7)
Фізичний маятник можна розглядати як такий, що складається з матеріальних точок, що коливаються, а кожну точку – як окремий математичний маятник з відповідним періодом коливань. При цьому можна вказати таку точку, яка буде мати такий період коливань, що відповідатиме періоду коливань фізичного маятника. Звідси випливає, що зведена довжина фізичного маятника – це довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника.
Відношення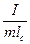 
вимірюється в одиницях довжини і називається зведеною довжиною фізичного маятника 
.
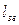Таким чином, підставляючи в (13.7)
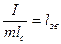, (13.8)
дістанемо
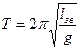. (13.9)
Формула (13.9) така ж сама, як і формула для періоду коливань математичного маятника при його довжині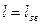 
.
Згідно з теоремою Штейнера момент інерції маятника відносно осі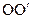 
, що знаходиться на відстані 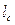від центра мас,
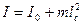, (13.10)
де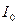 
- момент інерції цього ж маятника відносно осі, що проходить через його центр мас і паралельна до осі 
.
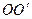З урахуванням теореми Штейнера формула (13.8) для зведеної довжини фізичного маятника набуває вигляду
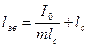(13.11)
З (13.11) видно, що зведена довжина, а відповідно, і період коливань фізичного маятника прямує до нескінченності при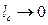 
. Іншими словами, при підвішуванні фізичного маятника в точці, що збігається з його центром мас, маятник коливатися не буде. У міру віддалення точки підвісу маятника від центра мас (у міру збільшення 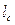) його зведена довжина (а значить, і період коливань) спочатку зменшується, досягаючи мінімуму, а потім монотонно зростає (рис.13.2).
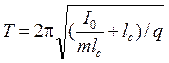(13.12)
