Основні теоретичні відомості

Будь-якіреальні коливання відбуваються з втратами енергії коливальної системи на роботу проти сил опору середовища, сил тертя. Амплітуда таких коливань з часом зменшується, і коливання згасають. При невеликих швидкостях руху для механічних коливань сила опору (тертя) 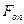пропорційна швидкості і завжди напрямлена проти руху тіла, тобто

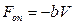, (14.1)

де b – коефіцієнт опору (тертя).

Таким чином у випадку згасаючих коливань на тіло, крім квазіпружної сили (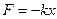), діє сила опору (тертя) (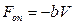). Тоді основний закон динаміки набуває вигляду 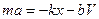(тіло рухається вздовж осі ОХ),

або 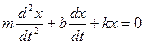, звідки .

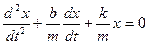Позначимо в останньому рівнянні 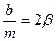і назвемо β коефіцієнтом згасання. Оскільки 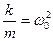(ω₀ – частота коливань за відсутності опору (тертя)), то

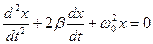. (14.2)

Рівняння (14.2) є диференціальним рівнянням згасаючих коливань.

Розв’язком рівняння (14.2) є така функція ()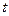

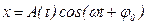, (14.3)

де 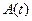– амплітуда згасаючих коливань,

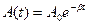; (14.4)

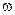– циклічна частота згасаючих коливань;

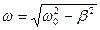. (14.5)

А₀ – амплітуда в початковий момент часу t =0; е – основа натуральних логарифмів.

З цього рівняння видно, що амплітуда згасаючих коливань зі зміною часу зменшується за експоненціальним законом.