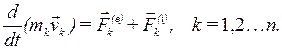Теорема об изменении количества движения системы

Для каждой точки системы, находящейся под действием внеш­них и внутренних сил, имеем:

Проведя суммирование по всем точкам системы, получим:

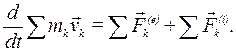
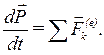Используя свойства внутренних сил системы и определение количе­ства движения системы 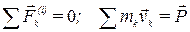, окончательно имеем:

Теорема об изменении количества движения системы: производ­ная по времени от количества движения системы равна вектор­ной сумме всех внешних сил, действующих на систему.

В другой форме теорема выглядит так: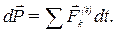

Дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему.

Теорема импульсов в конечной (интегральной) форме:

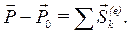
Изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время.