Пусть у некоторой выбранной точки D тела наблюдается плоское напряжённое состояние (рис. 33а,б).
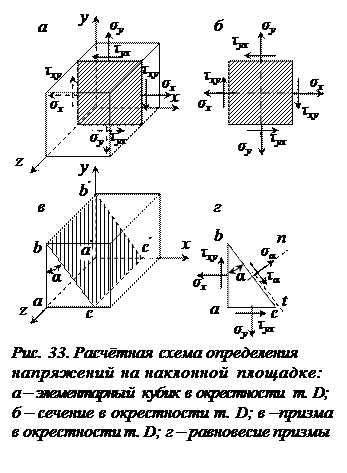 Выделим в окрестности точки призму abca'b'c' (рис. 33в), на грани bb'с′с которой (рис. 33г) действует нормальное напряжение σα и касательное τα (п – нормаль к этой грани, t – касательная). Рассмотрим равновесие данной призмы, приняв площадь наклонённой грани bb'с'с за dА. Тогда площадь грани abb'a', перпендикулярной оси х – dAcosα, а грани aa′c′c, перпендикулярной оси у – dAsinα. На грани abb'a', относительно которой на угол α повернута площадка bb'с′с, направление касательного напряжения τху = τ принято положительное.
Выделим в окрестности точки призму abca'b'c' (рис. 33в), на грани bb'с′с которой (рис. 33г) действует нормальное напряжение σα и касательное τα (п – нормаль к этой грани, t – касательная). Рассмотрим равновесие данной призмы, приняв площадь наклонённой грани bb'с'с за dА. Тогда площадь грани abb'a', перпендикулярной оси х – dAcosα, а грани aa′c′c, перпендикулярной оси у – dAsinα. На грани abb'a', относительно которой на угол α повернута площадка bb'с′с, направление касательного напряжения τху = τ принято положительное.
Сумма проекций всех сил на нормаль п:
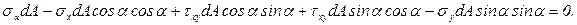
Приняв τху= τух= τ и сократив на dА, получим формулу для определения нормальных напряжений на площадке bb'с′с:
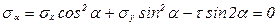 . (6.11)
. (6.11)
Проецируя все действующие силы на направление касательной t к наклонной площадке, получим:
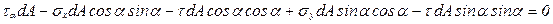 .
.
После несложных преобразований получим формулу для определения касательных напряжений на площадке bb'с′с:
|
|
|
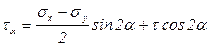 . (6.12)
. (6.12)
Формула для определения положения главных площадок, т. е. площадок, на которых касательные напряжения равны нулю, следует из выражения (6.12) при 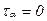 :
:
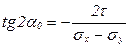 . (6.13)
. (6.13)
Углы α0 и 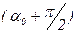 ,найденные по формуле (6.13), определяют положение главных площадок около анализируемой т. А. Подстановкой найденных значений углов α0 и
,найденные по формуле (6.13), определяют положение главных площадок около анализируемой т. А. Подстановкой найденных значений углов α0 и 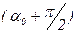 в выражение (6.11) для напряжений σα получим значения главных напряжений (σ2 = 0):
в выражение (6.11) для напряжений σα получим значения главных напряжений (σ2 = 0):
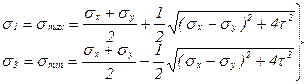 . (6.14)
. (6.14)
Максимальное значение касательных напряжений в теле:
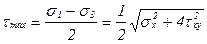 . (6.15)
. (6.15)
Значение 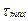 возникает на площадке, параллельной вектору
возникает на площадке, параллельной вектору 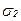 и делящей пополам угол между первой и третьей главными площадками.
и делящей пополам угол между первой и третьей главными площадками.
 2015-10-16
2015-10-16 389
389








