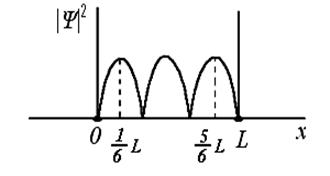
На рисунке приведена картина распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками. Вероятность обнаружить электрон на отрезке 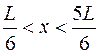 равна...
равна...
 | ВАРИАНТЫ ОТВЕТОВ: 1)  ; 2) ; 2) 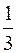 ; 3) ; 3) 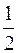 ; 4) ; 4) 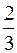 ; 5) ; 5) 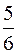 . . |
_ _ _ _ _ __ _ _ _ _ _ _ _ __ _
Указание к заданиям № 51 -55
Для частицы, находящейся в одномерной «потенциальной яме» с бесконечными стенками и плоским дном волновая функция Ψn (х) имеет следующий вид: 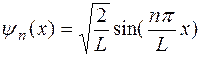 , где L – ширина «потенциальной ямы»,
, где L – ширина «потенциальной ямы»,
n – главное квантовое число (номер квантового состояния), которое характеризует энергетический уровень. В этом случае плотность вероятности 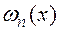 будет иметь вид:
будет иметь вид: 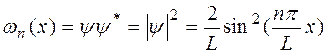 ,
,
где знак * означает комплексное сопряжение.
На участке 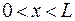 волновая функция Ψn (х) имеет n экстремумов, а функция плотности вероятности
волновая функция Ψn (х) имеет n экстремумов, а функция плотности вероятности 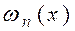 имеет n максимумов.
имеет n максимумов.
Вероятность 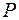 обнаружить электрон на участке (
обнаружить электрон на участке (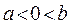 ) вычисляется по формуле:
) вычисляется по формуле: 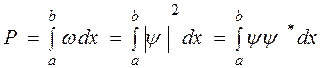 .
.
При этом вероятность 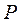 обнаружить электрон на всем участке L (
обнаружить электрон на всем участке L (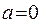 ,
, 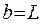 ) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой
) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой 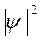 на всем участке L (
на всем участке L (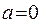 ,
, 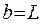 ) равна единице, а вероятность обнаружить электрон на интервале (
) равна единице, а вероятность обнаружить электрон на интервале (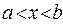 ) равна отношению площадей под кривой
) равна отношению площадей под кривой 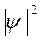 на этом интервале (
на этом интервале (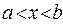 ) и на всем интервале (
) и на всем интервале (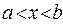 ) для
) для 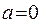 ,
, 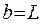 .
.
|
|
|
 2015-10-16
2015-10-16 730
730







