Типический (стратифицированный, расслоенный, районированный) отбор

Типический отбор используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или подотрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом.

Наиболее часто применяется так называемое пропорциональное размещение (пропорциональная типическая выборка), когда количество отбираемых в выборку единиц пропорционально удельному весу данной группы по числу единиц в генеральной совокупности, т.е. число наблюдений по каждой группе определяется по формуле ,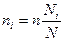

где 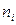– число наблюдений из 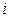-й типической группы;

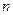− общий объём выборки;

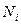– объём 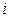-й типической группы в генеральной совокупности;

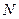– объём генеральной совокупности.

При отборе пропорционально численности группы

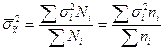. В этом случае средняя ошибка средней:

- при повторном отборе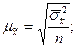

- при бесповторном отборе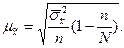

Пример 5. Для определения средней заработной платы рабочих завода была произведена 20%-ная бесповторная выборка по цехам с отбором единиц пропорционально численности групп.

Цех	Объём выборки, чел, ni	Средняя заработная плата, руб.,	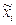Среднее квадратическое отклонение, руб.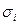
		26 873
		27 886
		28 900
Итого		-	-

С вероятностью 0,997 (t=3) определить пределы, в которых находится заработная плата всех рабочих завода.

Решение:

1. Находим общую выборочную среднюю заработную плату:

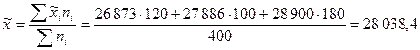руб.

2. Рассчитаем среднюю из групповых дисперсий:

.

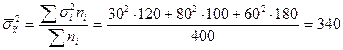3. Определяем среднюю ошибку выборочной средней заработной платы 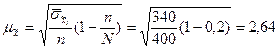руб.

4. Находим предельную ошибку выборочной средней заработной платы

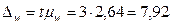руб.

5. Определяем пределы изменения генеральной средней

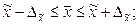
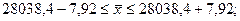
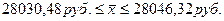
Средняя ошибка доли при пропорциональном типическом отборе:

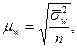
где ;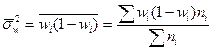

- при бесповторном отборе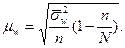

Второй вариант выбора единиц в типическую группу пропорционально внутригрупповой дифференциации признака, т.е. оптимальное размещение (непропорциональная типическая выборка). Расчёт объёма выборки из каждой типической группы производится по формуле ,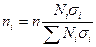

где 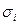– среднее квадратическое отклонение признака в i-й группе генеральной совокупности.

Данная формула получена следующим образом:

,

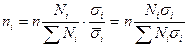где 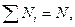а 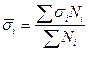– средняя из групповых средних квадратических отклонений.

Средняя ошибка средней непропорциональной типической выборки:

- при повторном отборе ,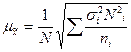

- при бесповторном отборе .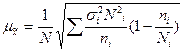

Пример 6. 10%-ный бесповторный типический отбор рабочих предприятия, пропорциональный дифференциации признака (число дней временной нетрудоспособности), привел к следующим результатам:

Цех	Всего рабочих, чел, Ni	Дисперсия числа дней временной нетрудоспособности,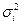
	1 000
	1 400
Итого	3 200	-

С вероятностью 0,954 определить предельную ошибку выборки.