Средняя величина – типическая характеристика совокупности (одна характеризует множество).
Классы средних величин: степенные (средняя арифметическая, средняя гармоническая. 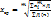 ); структурные (мода, медиана, квартили, децили, перцентили).
); структурные (мода, медиана, квартили, децили, перцентили).
Виды степенных средних:
| Степ. ср. | Показ. степени | Формула расчета | |
| Простая | Взвешенная | ||
| Гармон. | -1 | 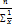
| 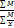
|
| Геом. | 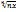
| 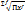
| |
| Арифм. | 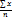
| 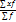
| |
| Квадратич. | 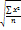
| 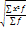
|
П – произведение; х – значение признака; М – сумма f; f – частота повторений х.
Если в формуле неизвестен числитель – применяется арифм., знаменатель – гарм.
Ср.гарм. для расчета показателей анализа рядов динамики.
Квадратич. – для показателей вариации.
Свойства ср.арифм.: если все индивид. знач. признака ↑ или ↓ в i раз, то ср.знач. нового признака ↑ или ↓ в i раз; если все варианты усредняемого признака ↑ или ↓ на число А, то ср.арифм. ↑ или ↓на А; если все веса всех осредняемых вариантов ↑ или ↓ в К раз, то ср. не изм.; нулевое свойство средней: 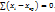
 2015-10-16
2015-10-16 413
413








