Для установления связи мы будем использовать фазовые диаграммы, которые принято использовать при анализе работы различных машин. Мы можем показать эту связь на примере любого типа машин: механических, термодинамических, электрических, электро-магнитных и др. Для простоты изложения воспользуемся обычным маятником (рис. 3.4).
Полная энергия маятника, состоящего из "пружины" и "массы" тела, будет при отсутствии "диссипативных" сил постоянна и состоять из "кинетической" и "потенциальной" энергии и еще какой-то "связной" энергии.
Наш "маятник" состоит из массы (размещен на тележке, которая катается без трения) и соединен с пружиной, которая обладает жесткостью K. В начальном положении сила натяжения-сжатия пружины равна нулю. Оттянем пружину до некоторой отметки на оси F, т.е. сообщим системе некоторое количество энергии, которое и будет "свободной" энергией. Отпустим тележку - она начнет совершать гармоническое колебание около положения равновесия. Общая и свободная энергия (из-за отсутствия диссипации) будут сохраняться, а "потенциальная" и "кинетическая" энергия будут переходить друг в друга. При этих взаимных переходах представляющая точка D будет перемещаться на отрезке 1-3.
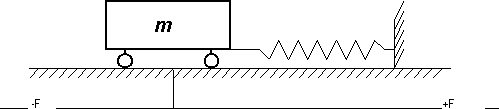
Рис. 3.4. Обычный маятник
Теперь мы должны "отождествить" наши точки 2 и 3 с точкой D; будем считать, что точка D находится в точке B, когда свободная энергия является "потенциальной" энергией; когда точка D находится в точке 3, то вся свободная энергия является "кинетической". Считая "кинетическую" и "потенциальную" энергию "компонентами" свободной энергии, мы можем рассматривать свободную энергию как векторную сумму своих компонент. Поскольку угол между кинетической и потенциальной энергией - прямой, а свободная энергия - постоянна - инвариант, то представляющая точка D будет описывать окружность (рис. 3.5).
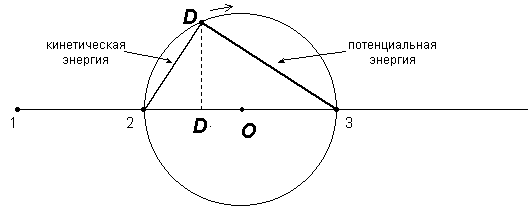
Рис. 3.5. "Гармоническое колебание" обычного маятника
Когда точка D находится в точке 2 - вся свободная энергия находится в форме потенциальной энергии. Когда D проходит через центр окружности, мы имеем равенство кинетической и потенциальной энергии. Приход в точку 3 соответствует пробеганию тележки с максимальной скоростью через нейтральное положение пружины - вся свободная энергия представлена в форме кинетической энергии. При движении по нижней полуокружности точки D происходит сжатие пружины. В точке 2 вся свободная энергия в потенциальной форме сжатия пружины. Следующий оборот точки D возвращает систему в исходное состояние.
 2015-10-16
2015-10-16 570
570








