Cлучайные ошибки измерений

Если повторять несколько раз измерения одной и той же физической величины (например, веса или, скажем, времени падения грузика), стараясь при этом сохранить все условия опыта постоянными, то, тем не менее, полученные результаты будут обязательно несколько отличаться друг от друга (если, конечно, для результатов каждого измерения записать достаточное количество значащих цифр). Тому существует множество разных причин, которые практически невозможно учесть. Как пример: неточности в фиксации времени включения и выключения секундомера, которые, кстати, важны для точного определения интервалов времени не только при физических измерениях, но и во многих других случаях, в частности, на спортивных соревнованиях. Как уже указывалось ранее, соответствующие ошибки называют случайными ошибками.

Со случайными изменениями некоторых величин мы встречаемся и в повседневной жизни, например, многократно отмечая время, которое требуется, чтобы доехать до нужного пункта. Случайные величины важны для многих разделов естествознания, например для молекулярной физики при измерениях скорости теплового движения молекул газа или в ядерной физике при изучении закономерностей радиоактивности. Для количественного описания всех таких случайно изменяющихся величин используют хорошо разработанные методы теории вероятностей. Эти методы позволяют строго определить не только средние и наиболее вероятные значения величин, но и вероятности отклонений от этих значений.

Среднее значение любой случайной величины х, а данном случае результатов нескольких последовательных её измерений (x₁, x₂, x_3…x_n), определяют как среднее арифметическое значение x по формуле:

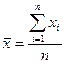, (5)

где n – число измерений.

Далее необходимо установить тот интервал значений (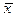 - D x ≤ x ≤ 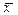+ D x), так называемый доверительный интервал, за пределы которого с обусловленной доверительной вероятностью ρ(Δ x) (определяющей коэффициент надежности полученных результатов измерения) не должны выходить значения x.

Доверительная вероятность ρ(Δ x) в случае непрерывного распределения значений x определяется как:

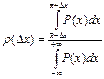, (6)

где P (x) – плотность вероятности реализации значений x в диапазоне от x до x + dx, причем знаменатель в этом выражении обычно принимается равным 1 (условие нормировки).

В теории вероятностей строго обосновывается, что с той же вероятностью ρ(Δ x) за пределы этого интервала не будут выходить средние значения x, определенные в различных сериях измерений, в том числе проводимых разными экспериментаторами или на разных, но однотипных установках.

Еще важнее, что эти две величины (доверительный интервал и доверительная вероятность) однозначно определяют отличие измеренного значения x от истинного значения той же физической величины a. Именно в их определении и состоит основная задача математической обработки результатов измерений.

Для решения этой задачи необходимо помимо 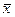найти среднюю квадратичную ошибку измерений 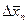в данной серии опытов, которая определяется по следующей формуле:

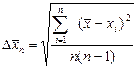. (7)

Вычисление средней квадратичной, а не, как часто делается, средней арифметической ошибки измерений:

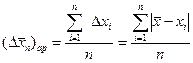, (8)

позволяет более корректно и просто определить затем доверительный интервал и доверительную вероятность, как это будет показано в дальнейшем.

Таким образом, при n ®¥, 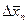®0 и случайную ошибку измерения можно в принципе сделать столь угодно малой величиной, что однако потребует бесконечно долгого процесса измерения.

Определение доверительного интервала для случайной ошибки и, соответственно, отличие среднего значения 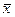от истинного значения этой величины а для заданного значения доверительной вероятности r(D x) очевидно требует знания конкретного вида функции распределения P_i (x_i), т.е. функции реализации определенных значений x_i.

Рассмотрим вначале наиболее простой для математической обработки, но сложный для практического осуществления случай достаточно большого числа измерений. Строго говоря, для этого необходимо, чтобы n ®¥ и дискретная функция распределения P_i (x_i) переходила в непрерывную функцию плотности вероятности P (x). Однако, как будет показано далее, для этого достаточно n > 100 или даже n > 30. При этом обычно реализуется функция нормального распределения или функция Гаусса, названная так в честь великого немецкого математика, впервые установившего вид этой функции:

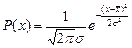. (9)

Здесь использована новая величина s – среднестатистический предел среднеквадратичной ошибки одного измерения при очень большом количестве измерений. Квадрат этой величины s², однозначно определяющей ширину функции распределения для ошибок измерения и вообще распределения случайных величин, называют нормой или дисперсией распределения.

Для обоснования применимости формулы Гаусса необходимо выполнение трех положений, а именно:

— ошибки измерения могут принимать непрерывный ряд значений,

— при достаточно большом числе измерения ошибки одинаковой абсолютной величины, но разного знака, встречаются одинаково часто

— большие ошибки наблюдается реже, чем меньшие.

Тогда измеренные значения величины x, будут находиться внутри доверительного интервала (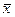 - D x ≤ x ≤ 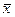+ D x) с доверительной вероятностью r(D x), определяемой по формуле:

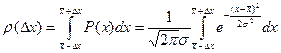. (10)

При этом, чем больше требуется доверительная вероятность r(D x) и, соответственно, надежность того, что измеренные значения x отличаются от истинного значения этой величины а не более, чем на ±D x, тем шире по отношению к s становится доверительный интервал. Так, если, например, требуется, чтобы r(D x) = 0,7; 0,95; 0,98 или 0,999, то соответствующие доверительные интервалы будут равны s; 2s; 2,3s или 3,3s.

Для выбора конкретного значения доверительной вероятности r(D x), определяющей значения доверительного интервала ±D x, необходимо понимать, насколько опасен выход за пределы этого интервала, вероятность которого, очевидно, равна 1– r(D x). Такие задачи возникают на практике, например, при отбраковке изделий, выпускаемых в машиностроительной промышленности, по их габаритам или другим параметрам.

Реально очень трудно осуществить (по причинам большой длительности и малой продуктивности) вышеуказанный идеализированный случай, требующий, чтобы число измерений было, по крайней мере, больше тридцати. Поэтому необходимо рассмотреть реальный, но более сложный для анализа случай относительно небольшого числа измерений (3 < n < 10). Интуитивно понятно, что в этом случае возникают повышенные требования к доверительному интервалу (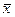 - D x; 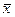+ D x) при заданном значении r(D x), то есть он становится шире. Увеличение числа измерений, наоборот, сужает этот интервал.

На опыте часто измеряют физические величины, которые могут принимать лишь дискретные значения, а число этих измерений конечно. В ряде случаев вероятность реализации определенных значений таких величин хорошо описывается распределением Пуассона (знаменитый французский математик и физик).

Для многих лабораторных работ, когда число измерений не велико, распределение погрешностей описывается еще более сложными, специальными гамма–функциями (распределение Стьюдента или “t”– распределение. “Стьюдент” – это псевдоним английского математика Уильяма Сита Госсета.). Для такого распределения с высокой точностью вычислены и затабулированы так называемые коэффициенты Стьюдента a (таблица №1). Они определяют отношение доверительного интервала D x к средней квадратичной ошибке 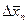для данной серии измерений и определенных значений n и r(D x), то есть:

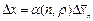. (11)

Коэффициенты Стьюдента a. Таблица №1.

n (число измерений)	Доверительная вероятность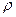
0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999
21-24 26-27	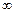0,16 0,14 0,14 0,13   0,13 0,13 0,13 0,13 0,13   0,13 0,13 0,13 0,13 0,13   0,13 0,13 0,13 0,13 0,13   0,13 0,13 0,13 0,13 0,13 0,13   0,13 0,13 0,13 0,13	0,33 0,29 0,28 0,27   0,27 0,27 0,26 0,26 0,26   0,26 0,26 0,26 0,26 0,26   0,26 0,26 0,26 0,26 0,26   0,26 0,26 0,26 0,26 0,26 0,26   0,26 0,25 0,25 0,25	0,51 0,45 0,42 0,41   0,41 0,40 0,40 0,40 0,40   0,40 0,40 0,40 0,39 0,39   0,39 0,39 0,39 0,39 0,39   0,39 0,39 0,39 0,39 0,39 0,39   0,39 0,39 0,39 0,39	0,73 0,62 0,58 0,57   0,56 0,55 0,55 0,54 0,54   0,54 0,54 0,54 0,54 0,54   0,54 0,54 0,53 0,53 0,53   0,53 0,53 0,53 0,53 0,53 0,53   0,53 0,53 0,53 0,52	1,00 0,82 0,77 0,74   0,73 0,72 0,71 0,71 0,70   0,70 0,70 0,70 0,69 0,69   0,69 0,69 0,69 0,69 0,69   0,69 0,69 0,68 0,68 0,68 0,68   0,68 0,68 0,68 0,67	1,38 1,06 0,98 0,94   0,92 0,90 0,90 0,90 0,88   0,88 0,87 0,87 0,87 0,87   0,87 0,86 0,86 0,86 0,86   0,86 0,86 0,86 0,86 0,86 0,85   0,85 0,85 0,85 0,84	2,0 1,3 1,3 1,2   1,2 1,1 1,1 1,1 1,1   1,1 1,1 1,1 1,1 1,1   1,1 1,1 1,1 1,1 1,1   1,1 1,1 1,1 1,1 1,1 1,1   1,1 1,0 1,0 1,0	3,1 1,9 1,6 1,5   1,5 1,4 1,4 1,4 1,4   1,4 1,4 1,4 1,4 1,3   1,3 1,3 1,3 1,3 1,3   1,3 1,3 1,3 1,3 1,3 1,3   1,3 1,3 1,3 1,3	6,3 2,9 2,4 2,1   2,0 1,9 1,9 1,9 1,8   1,8 1,8 1,8 1,8 1,8   1,8 1,7 1,7 1,7 1,7   1,7 1,7 1,7 1,7 1,7 1,7   1,7 1,7 1,7 1,6	12,7 4,3 3,2 2,8   2,6 2,4 2,4 2,3 2,3   2,2 2,2 2,2 2,2 2,1   2,1 2,1 2,1 2,1 2,1   2,1 2,1 2,1 2,0 2,0 2,0   2,0 2,0 2,0 2,0	31,8 7,0 4,5 3,7   3,4 3,1 3,0 2,9 2,8   2,8 2,7 2,7 2,7 2,6   2,6 2,6 2,6 2,6 2,5   2,5 2,5 2,5 2,5 2,5 2,5   2,4 2,4 2,4 2,3	63,7 9,9 5,8 4,6   4,0 3,7 3,5 3,4 3,3   3,2 3,1 3,1 3,0 3,0   2,9 2,9 2,9 2,9 2,9   2,8 2,8 2,8 2,8 2,8 2,8   2,7 2,7 2,6 2,6	636,6 31,6 12,9 8,6   6,9 6,0 5,4 5,0 4,8   4,6 4,5 4,3 4,2 4,1   4,0 4,0 4,0 3,9 3,9   3,8 3,7 3,7 3,7 3,7 3,7   3,6 3,5 3,4 3,3

Из таблицы 1 следует, что при доверительной вероятности r(D x) > 0,7 доверительный интервал D x всегда несколько превышает значение 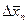, но для r(D x)=0,7 по мере увеличения числа измерений n стремится к этому значению, причем их различие становится незначительным (меньше 10%) уже при n ³ 7. Аналогичное, но более медленное уменьшение a наблюдается и для более высоких значений r(Dx)= 0,95; 0,98; 0,999. Для этих значений r, чтобы достаточно приблизиться к предельным значениям a (2; 2,3; 3,3), соответствующим функции Гаусса, необходимо значительно большее число измерений (n > 15, 20 и 40). В большинстве лабораторных работ число измерений (3 < n £ 10), а доверительная вероятность r(D x) принимается равной 0,95, так что соответствующие коэффициенты Стьюдента изменяются от 4,3 до 2,3. Если значения доверительной вероятности не указаны, то её обычно выбирают равной 0,7.

Таким образом, окончательный результат измерений с указанием доверительной вероятности в лабораторных практикумах следует представлять в виде:

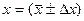, (12)

где за скобкой указывают единицу измерения данной величины в общепринятой международной системе единиц (СИ).

При этом необходимо, чтобы среднее значение 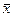и доверительный интервал D x были записаны в одних и тех же единицах и с одинаковой точностью. Доверительный интервал D x обычно записывают в виде двух (реже одной) значащих цифр, округляя последующие цифры. Если число n измерений совсем невелико (менее 5 – 6), что имеет место в большинстве лабораторных работ, то достаточно округления доверительного интервала до первой значащей цифры, и только если она является единицей – до двух. При большем числе измерений n ~ 10, как правило, следует оставлять одну значащую цифру, если только она больше трёх. При ещё большем числе измерений (n ~ 30 и более) оставляются две значащие цифры. 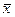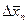Предварительные вычисления и следует проводить, разумеется, с несколько более высокой точностью.

Всё вышеуказанное справедливо прежде всего для прямых измерений, когда на опыте непосредственно измеряется интересующая нас физическая величина. При косвенных измерениях, когда эта величина определяется по известной формуле, в которую входят несколько других измеряемых на опыте независимых величин, необходимо провести дополнительный анализ общей ошибки измерения. Если искомая величина y = ¦(x₁, x₂….x_k), то есть является известной функцией нескольких непосредственно измеряемых величин x_i, то её среднее значение определяется как 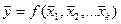. Если в данном опыте преобладают приборные ошибки, тооценку абсолютной D y и относительной dошибки измерения следует производить по формулам:

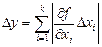, (13)

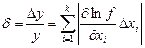. (14)

Если, наоборот, в этих измерениях преобладают случайные ошибки, то расчет общей ошибки производят по формуле:

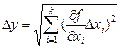. (15)

Вопрос о том, какими формулами пользоваться, решают при анализе результатов измерений. Если отклонения большинства из результатов измерений от среднего арифметического значения не превышает абсолютную ошибку используемых приборов, то расчет производят по формулам (13) и (14), а в противоположном случае по формуле (15). В общем случае случайные D x_сл и приборные ошибки D x_np складываются по общему закону сложения всех случайных величин, а именно:

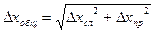. (16)

Поэтому, если одна из этих ошибок в три и более раз превышает другую ошибку, то последняя из этих ошибок будет очень слабо влиять на общую точность измерения. Исходя из этих соображений обычно и выбирается необходимое число измерений n, поскольку нет никакого смысла стремиться получить случайную ошибку значительно меньше приборной ошибки.

Наглядной иллюстрацией систематических и случайных ошибок могут служить результаты стрельбы из различных видов оружия, в том числе на спортивных соревнованиях. Так, если имеется только систематическая ошибка (сбит прицел, неправильное прицеливание или расчеты), то все пули (снаряды, стрелы, бомбы и т.д.) попадут в одно и то же место, но смещенное от центра мишени или цели. Наоборот, если существуют только случайные ошибки, то будет значительный разброс в местах попадания («плохая кучность»), но усредненное отклонение от центра мишени (или цели) будет стремиться к нулю. Реально, конечно, наблюдаются оба вида ошибок, но один из них обычно существенно преобладает над другим.

Теория вероятностей полезна и для правильного построения графиков на основе полученных экспериментальных данных. Недопустимо рисовать изломанную кривую, точно проходящую через экспериментальные точки: следует провести такую плавную линию, чтобы отклонение экспериментальных точек от нее в разные стороны приблизительно компенсировали друг друга. По методу наименьших квадратов построение графика экспериментальной зависимости y=¦(x) следует проводить таким образом, чтобы свести к минимуму сумму квадратичных отклонений 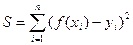экспериментальных точек y_i от проводимой кривой f(x_i), где i - номер экспериментальной точки, n – число экспериментальных точек.

Для построения графика кривой по экспериментальным точкам вначале подбирается функциональная зависимость определённого вида (линейная: y=a+bx, квадратичная: y=a+bx+cx², экспоненциальная: y = a+be^x и т.д.), которая предположительно наилучшим образом соответствует экспериментальным данным, и определяются значения её параметров a,b,c. При этих значениях функция S должна минимальна, то есть её частные производные по этим параметрам должны быть равны нулю: 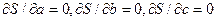. Решая полученную систему уравнений, сначала находят значения этих параметров, а затем и значение S. Сравнивая значения S, полученные таким же образом для разного вида функций f(x), выбирают функцию, для которой S будет минимальна – этой функцией и аппроксимируются полученные экспериментальные данные.

Следует отметить, что разработаны способы, с помощью которых можно достаточно просто оценить наиболее подходящую функцию y = f(x) для описания известных экспериментальных данных. Кроме того, существует компьютерная программа Grapher, которая даёт возможность подбирать необходимые функции с соответствующими параметрами для приближения экспериментально полученных точек x_i и y_i. Добавим, что удобно использовать для построения графиков такие координаты, при которых график функции представляет собой прямую (эти координаты следует выбирать на основании подобранной функции y=f(x)).

Методы теории вероятностей успешно используют и для планирования различных экспериментов, например по разработке технологии синтеза многокомпонентных материалов с оптимальными свойствами (электрическими, оптическими, механическими и др.), требующимися для их практических применений.

Прогресс физики и других разделов естествознания во многом определяется точностью экспериментов. В настоящее время достигнута поразительная точность при измерении ряда физических величин (расстояние, время и др.). Так, с помощью молекулярных генераторов и стандартов частоты удается осуществить такие молекулярные часы, что их ошибка составляет всего одну секунду за 10⁶ лет, т.е. относительная погрешность равна 10^-12%.

С очень высокой точностью измерена и такая важнейшая физическая величина как скорость распространения света в вакууме с = (299792458,0 ± 1,2) м/с. Это позволяет производить очень точные измерения больших расстояний: до Луны, планет Солнечной системы и других космических объектов.

На смену общеизвестного эталона метра в виде стержня, изготовленного из платиноиридиевого сплава и хранящегося в международной Палате мер и весов вблизи Парижа, пришел «оптический эталон». Он равен 1650763,73 длин волн оранжевой линии излучения атомов криптона, то есть на одном метре должно укладываться ровно столько длин волн этого излучения. Такой эталон примерно в 100 раз точнее прежнего и может быть легче воспроизведен в научных лабораториях. При обычных измерениях, например в физическом практикуме, конечно, не удается достичь таких прецизионнных точностей измерений, которые во многом определяются погрешностью используемых приборов. Вместе с тем при работе в практикуме нужно стремиться к уменьшению ошибок измерения, правильно производить их оценки и грамотно оформлять промежуточные и окончательные результаты измерений.