Указания к решению задания

под пунктом а):

1. Пользуясь правилом вычисления неопределенного интеграла суммы функций 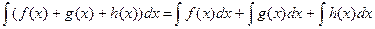, разложите данный интеграл на сумму неопределенных интегралов от каждой функции.

2. Вынесите постоянный множитель за знак интеграла там, где это необходимо.

3. Пользуясь табличными интегралами, вычислите полученные.

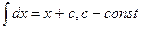
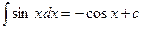
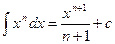
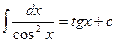
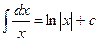
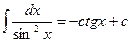
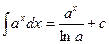
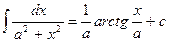
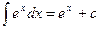
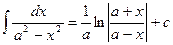
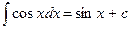
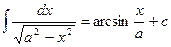
4. Для проверки найдите дифференциал получившейся функции и сравните его с подынтегральным выражением данного интеграла.

5. Сделайте вывод.

под пунктом б):

1. Избавьтесь от дроби, стоящей под знаком интеграла, деля каждое выражение в числителе на знаменатель, учитывая свойства корней и степеней:

,

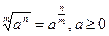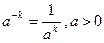
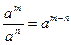
2. Пользуясь правилом вычисления неопределенного интеграла суммы функций 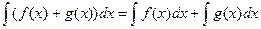, разложите данный интеграл на сумму неопределенных интегралов от каждой функции.

3. Вынесите постоянный множитель за знак интеграла там, где это необходимо.

4. Пользуясь табличными интегралами, вычислите полученные.

под пунктом в):

Введите новую переменную t =, тогда dt =, откуда dx=.

Подставьте найденные значения в данный интеграл, сведите его к табличному. Вычислите полученный. Вернитесь к подстановке.

Задачи № 21-25 Найти общее решение дифференциальных уравнений:

21. x+ y'=0

22. 4 x³- y'=0

23. (x+1)ydx=dy

24. 2xdx=3y²dy

25. y'=x²y-x²

Задачи № 26-30 Найти частное решение дифференциальных уравнений

26. x²dy=y²dx, если y=0,25 при x=0,1

27. 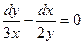, если y=5 при х=4

28. y'=3х², если y=5 при х=1

Задача № 29.

Показать, что функция у=х²+х удовлетворяет уравнению y'-2х=1