Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому 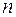 , а коэффициенты квадратичной формы не всегда являются вещественными числами.
, а коэффициенты квадратичной формы не всегда являются вещественными числами.
Квадратичной формой 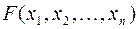 от
от 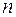 неизвестных
неизвестных 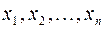 называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
Пример. Сумма 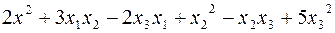 является квадратичной формой от трех неизвестных
является квадратичной формой от трех неизвестных 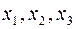 .
.
Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при 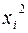 обозначаются через
обозначаются через 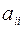 , а коэффициенты при
, а коэффициенты при 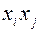 через
через 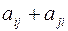 , причем
, причем 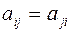 Член
Член 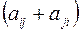
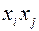 записывается в виде
записывается в виде 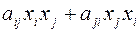 . После этих преобразований квадратичную форму можно записать в виде:
. После этих преобразований квадратичную форму можно записать в виде:
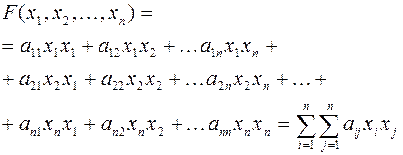
Матрица:
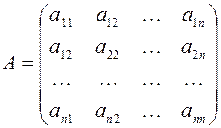
называется матрицей квадратичной формы 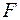 . Так как
. Так как 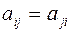 , то
, то 
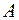 – симметричная матрица.
– симметричная матрица.
С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.
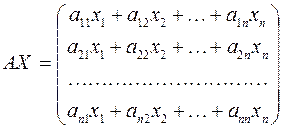 ,
,
где 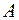 – матрица квадратичной формы,
– матрица квадратичной формы, 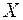 – матрица–столбец неизвестных:
– матрица–столбец неизвестных:

Приведенные выкладки показывают, в частности, что если 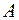 – симметрическая матрица, то выражение
– симметрическая матрица, то выражение 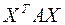 является квадратичной формой от неизвестных
является квадратичной формой от неизвестных 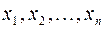 , т.е. квадратичная форма является результатом скалярного произведения матриц
, т.е. квадратичная форма является результатом скалярного произведения матриц 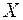 и
и 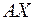 . Матричная форма записи квадратичной формы имеет вид
. Матричная форма записи квадратичной формы имеет вид 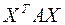 . Если
. Если 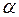 – произвольный
– произвольный 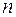 – мерный вектор, то после подстановки в квадратичную форму
– мерный вектор, то после подстановки в квадратичную форму 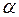 вместо
вместо 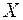 получится число
получится число 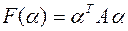 , которое называется значением квадратичной формы
, которое называется значением квадратичной формы 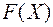 на векторе
на векторе 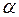 .
.
 2015-10-13
2015-10-13 672
672








