Часть
Прямая
Уравнение линии на координатной плоскости ху называется уравнение, которому удовлетворяют координаты х и у каждой точки этой линии и не удовлетворяют координаты ни одной точки, не лежащей на этой линии.
В общем случае уравнение линии может быть записано в виде
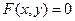
или, если это возможно, в явном виде
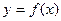 ,
,
где 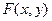 и
и 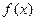 - некоторый формулы.
- некоторый формулы.
Виды уравнения прямой на плоскости.
Уравнение прямой с угловым коэффициентом. Углом наклона прямой называется угол α, отсчитываемый до прямой от положительного направления оси 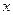 против часовой стрелки.
против часовой стрелки.
Тангенс этого угла tgα называется угловым коэффициентом прямой и обозначается k= tgα.
Y 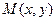
О 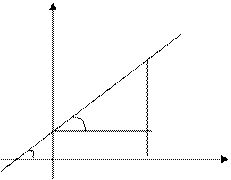 x (рис. 2)
x (рис. 2)
Пусть прямая отсекает на оси 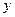 отрезок
отрезок 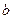 . Из рисунка очевидно, что
. Из рисунка очевидно, что
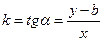 .
.
Отсюда следует, что
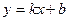 .
.
Это уравнение называется уравнением прямой с угловым коэффициентом.
Уравнением прямой с угловым коэффициентом k, проходящей через данную точку 
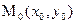


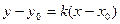 .
.
Это уравнение определяет пучок прямых, проходящих через точку 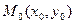 , кроме вертикальной прямой, имеющей уравнение
, кроме вертикальной прямой, имеющей уравнение 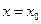 .
.
Уравнением прямой, проходящей через две данные точки 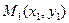 и
и 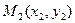 :
:
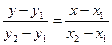 .
.
Уравнение прямой в отрезках:
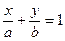 .
.
Общее уравнение прямой. Общим уравнением прямой на плоскости называется уравнение вида
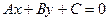 ,
,
где А, В, С- действительные числа, а А и В не равны одновременно нулю, т.е. 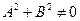 .
.
Уравнение прямой по точке и вектору нормали. В декартовой прямоугольной системе координат вектор 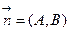 перпендикулярен прямой
перпендикулярен прямой 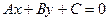 , компоненты которой являются координатами вектора.
, компоненты которой являются координатами вектора.
Уравнение прямой по точке и направляющему вектору. Каждый нулевой вектор 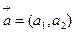 , компоненты которого удовлетворяют условию
, компоненты которого удовлетворяют условию 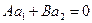 , называется направляющим вектором прямой
, называется направляющим вектором прямой 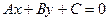 .
.
Углом между двумя параллельными прямыми 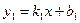 и
и 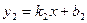 называется угол
называется угол 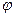 , образованный этими прямыми при пересечении и лежащий в диапазоне
, образованный этими прямыми при пересечении и лежащий в диапазоне 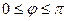 .
.
Обозначим 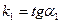 ;
; 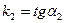 . Из рис. 2 видно, что
. Из рис. 2 видно, что 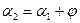 ,
, 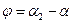 .
.
y 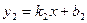
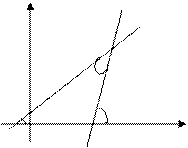 x (рис 2)
x (рис 2)
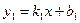
Тогда 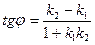 .
.
Если прямые 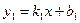 и
и 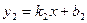 параллельны, то
параллельны, то 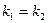 .
.
Равенство угловых коэффициентов – необходимое и достаточное условие параллельности двух прямых.
Если прямые перпендикулярны, то 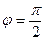 , то
, то 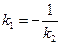 .
.
Справедливо также и обратное утверждение: для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратными по величине и противоположными по знаку.
Если прямые заданы общими уравнениями 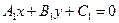 и
и 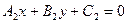 , то условие параллельности прямых:
, то условие параллельности прямых: 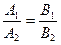 .
.
Условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных.
Пусть даны точка 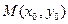 и прямая
и прямая 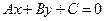 . Под расстоянием
. Под расстоянием 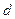 от точки М до прямой понимается длина перпендикуляра, опущенного из точки М на данную прямую (рис. 3).
от точки М до прямой понимается длина перпендикуляра, опущенного из точки М на данную прямую (рис. 3).
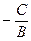 y
y 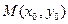
0  x рис. 3.
x рис. 3.
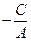
Расстояние между точкой и прямой 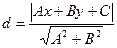 .
.
Часть
Кривые второго порядка
Окружностью называют геометрическое место точек, равноудаленных от точки, называемой центром окружности.
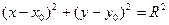 (1)
(1)
Уравнение (1.) называется нормальным уравнением окружности. В частности, уравнение окружности с центром в начале координат 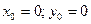 имеет вид
имеет вид 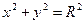 .
.
Каноническое уравнение эллипса 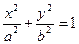 .
.
y 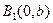
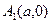
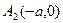
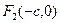
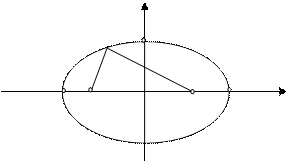
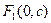
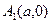 рис.1
рис.1
Пусть 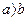 . Тогда числа
. Тогда числа 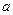 и
и 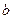 называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.
Центром эллипса называется точка пересечения его полуосей.
Точки 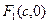 и
и 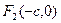 , где
, где 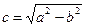 , называются фокусами эллипса, а отношение
, называются фокусами эллипса, а отношение 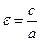 - его эксцентриситетом.
- его эксцентриситетом.
Эксцентриситет характеризует форму эллипса - чем величина 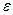 больше, тем эллипс более сжатый. Ясно, что
больше, тем эллипс более сжатый. Ясно, что 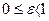 , причем, если
, причем, если 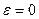 , то эллипс вырождается в окружность, для которой
, то эллипс вырождается в окружность, для которой 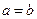 .
.
Сумма расстояний от любой точки эллипса до ее фокусов постоянна и равна 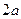 . То есть
. То есть 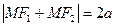 . Это характеристическое свойство эллипса часто принимают за определение эллипса.
. Это характеристическое свойство эллипса часто принимают за определение эллипса.
Если центр эллипса лежит не в начале координат, а в точке 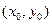 , то каноническое уравнение эллипса имеет вид
, то каноническое уравнение эллипса имеет вид
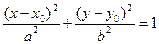 .
.
Если в каноническом уравнении эллипса 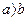 ,
,
то 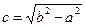 и фокусы располагаются по оси Оу, т.е.
и фокусы располагаются по оси Оу, т.е. 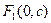 и
и 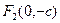 .
.
Каноническое уравнение гиперболы 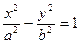 .
.
Гипербола имеет фокусы- точки 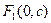 и
и 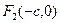 , в которых
, в которых 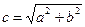 , а ее
, а ее
эксцентриситет 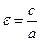 принимает любые значения, больше единицы.
принимает любые значения, больше единицы.
Вершины гиперболы- точки 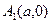 и
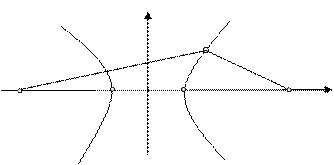
и 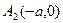 . График гиперболы на рис. 2.
. График гиперболы на рис. 2.
Для любой точки гиперболы 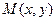 абсолютная величина разности ее расстояния до фокусов есть величина постоянная и равная
абсолютная величина разности ее расстояния до фокусов есть величина постоянная и равная 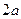 . То есть выполняется равенство
. То есть выполняется равенство 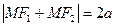 .
.
Это характеристическое свойство гиперболы часто принимают за определение гиперболы.
у 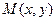
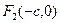
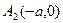
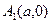
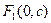 х
х
Рис. 2.5.
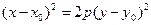 - уравнение, описывающее кривую, которая называется параболой относительно оси Оу. Точка
- уравнение, описывающее кривую, которая называется параболой относительно оси Оу. Точка 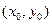 - вершина параболы.
- вершина параболы.
Если вершина параболы расположена в начале координат, то уравнение параболы принимает вид 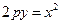 .
.
Величина 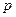 называется параметром параболы. Точка
называется параметром параболы. Точка 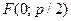 называется фокусом параболы, а прямая
называется фокусом параболы, а прямая 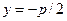 - ее директрисой.
- ее директрисой.
Можно показать, что парабола представляет собой множество всех точке плоскости, равноотстоящих от фокуса и от директрисы: 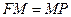 .
.
Это характеристическое свойство часто принимают за определение параболы.
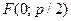 у
у 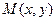
 директриса рис. 3.
директриса рис. 3.
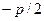
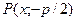 х
х
5. Рекомендуемое содержание отчета (для студента).
1. Название лабораторной работы.
2. Цель и задачи исследований.
3. Электронно-вычислительные средства для расчетов.
4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).
5. Выводы.
6. Анализ и защита лабораторной работы производится по результатам представленного студентами отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы, выполненные индивидуальные задания).
Преподаватель оценивает знание каждого студента.
Литература
 2015-10-16
2015-10-16 500
500








