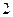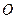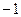2015-10-16
328
Понятие определенного интеграла, его геометрический смысл.
Пусть на отрезке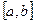 
определена некоторая функция 
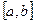(рис.1). Разобьем отрезок на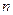 
частей точками 
.
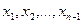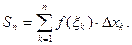
Функция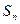 
называется интегральной суммой для функции 
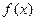на отрезке .
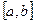Если существует предел интегральных сумм при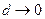 
(при этом 
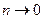), то он называется определенным интегралом от функции 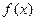в пределах от 
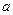до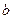 
, а функция 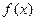называется интегрируемой на отрезке .
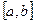Эту формулу можно записать в виде
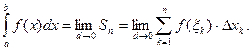
Числа 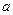и 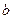называются соответственно нижним и верхним пределами интегрирования, а функция 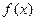, как и в случае неопределенного интеграла, называется подынтегральной функцией.
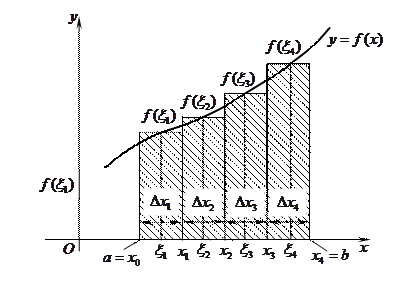
Рис.1. Разбиение площади под кривой функция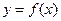
Геометрический смысл определенного интеграла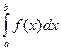 
состоит в том, что он по абсолютной величине численно равен площади фигуры (криволинейной трапеции), ограниченной графиком функции 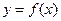, осью х и прямыми х = а и х= b.
Свойства определенного интеграла.
1. Определенный интеграл является числом, не зависящим от выбора обозначения переменной интегрирования, т.е.
|
|
|
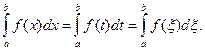
2. Если функция 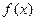определена в точке 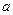, то
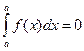
3. Если функция 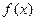интегрируема на отрезке 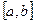, то при замене пределов интегрирования меняется знак.
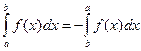
4. Если функци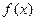и и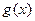 
интегрируемы на отрезке , 
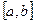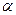и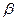 
- постоянные множители, то функция 
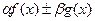тоже интегрируема на отрезке, причем
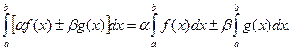
5. Если функция 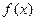интегрируема на отрезках 
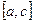и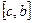 
, то она интегрируема и на отрезке 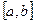, причем
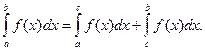
Геометрически это факт иллюстрируется рис.2
Рис.2. Разбиение площади под кривой на две фигуры.
Можно утверждать обратное. Если функция интегрируема на отрезке 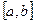, то она интегрируема и на любой части этого отрезка.
6. Если функция 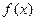непрерывна на отрезке 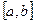, то она интегрируема на этом отрезке, причем существует точка 
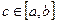такая, что справедливо равенство
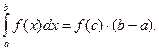
Это свойство, иллюстрируемое рис.10, часто называют теоремой о среднем значении или просто теоремой о среднем.
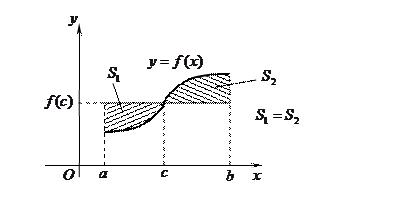
Формула Ньютона-Лейбница
Основная формула интегрального исчисления - формула Ньютона-Лейбница:
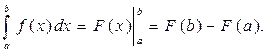
Пример. Вычислить определенные интегралы.
1. 
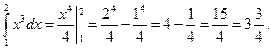
2. 
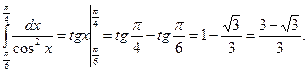
Вычисление площадей плоских фигур и объема тел вращения
Площади плоских фигур.
Пусть функция 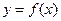неотрицательна и непрерывна на отрезке 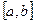. Тогда по геометрическому смыслу определенного интеграла площадь 
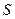под кривой 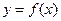на отрезке 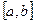численно равна определенному интегралу
.
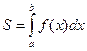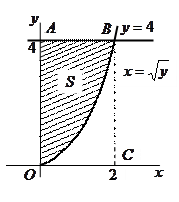
Пример. Найти площадь фигуры, ограниченной линиями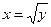 
, 
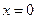, y=4.
Решение
Из чертежа очевидно, что искомая площадь 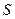криволинейного треугольника ОАВ равна разности двух площадей:
,
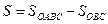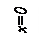
каждая из которых находится по геометрическому смыслу определенного интеграла.
Решая систему
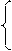
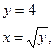
получаем, что точка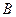 
пересечения прямой 
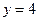и кривой 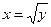имеют координаты (2; 4).
|
|
|
Тогда
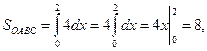
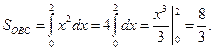
Окончательно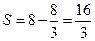 
(ед.2).
Пусть функция 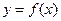неположительная и непрерывна на отрезке .
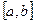Тогда площадь под осью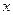 
вычисляется с учетом неположительности функции :
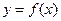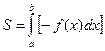, т.е.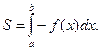 
Таким образом, если функция 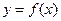неположительная на отрезке 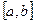, то площадь 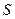над кривой 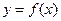на отрезке 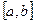отличается знаком определенного интеграла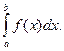 
Теорема упрощает решение задач на вычисление площадей плоских фигур.
Пусть на отрезке 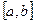заданы непрерывные функци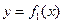и 
и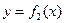 
такие, что 
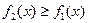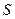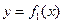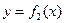. Тогда площадь фигуры, заключенной между кривыми и , на отрезке 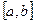вычисляется по формуле
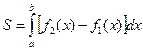. (1.1)
Проиллюстрируем теорему графически. Возможны несколько случаев расположения кривых на отрезке .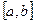
1. 
.
.
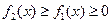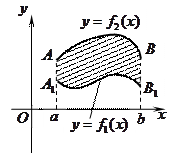
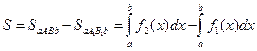2. 
.
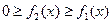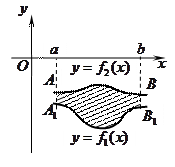
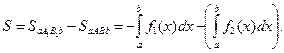
3. 
, 
.
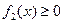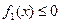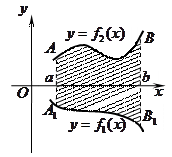
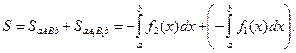
4. Общий случай сводится к частным случаям, рассмотренным выше, если разбить отрезок 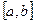на отдельные отрезки 
, 
, 
.
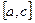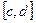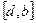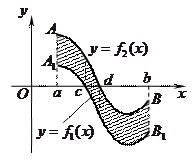
Пример. Найти площадь фигуры, ограниченной линиями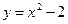 
, 
.
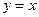Решение
Найдем координаты точек пересечения параболы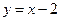 
и прямой 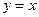. Решая систему из этих уравнений, получим точки (-1; -1) и (2; 2).
|
|
|
|
|
|
 |
На интегрируемом отрезке [-1; 2] выполняется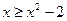 
. тогда по формуле (1.1) имеем
.
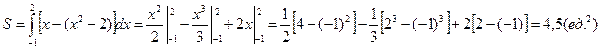Объемы тел вращения
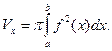(1.2)
Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями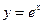 
, 
, , 
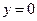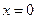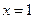вокруг оси 
.
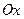Решение
Построим данную фигуру.
По формуле (1.2) искомый объем
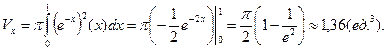
Формально заменяя в формуле (1.2) переменную 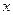на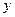 
, получаем формулу для объема 
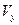тела, полученного от вращения криволинейной трапеции вокруг оси ординат
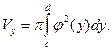
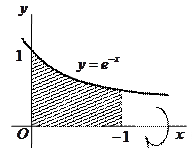
Методы вычисления определенного интеграла
Вычисление определенного интеграла производится в два этапа.
На первом этапе вычисляется первообразная, а затем (на втором этапе) в нее подставляется пределы интегрирования по формуле Ньютона-Лейбница.
Методы вычислении первообразной определенного интеграла аналогичны неопределенному интегрированию.
Особенности использования замены переменной и интегрирования по частям в определенном интеграле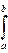 
ƒ(x) dx соответственно:
-при использовании замены t = u (x) изменение границ интегрирования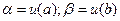 
;
-формула интегрирования по частям: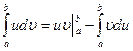 
.
Пример.
 |
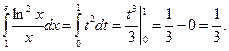
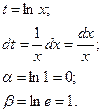
Пример.
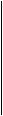
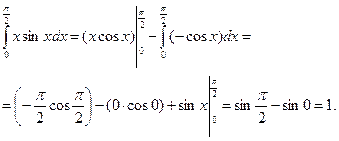
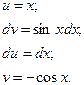
5. Рекомендуемое содержание отчета (для студента).
1. Название лабораторной работы.
2. Цель и задачи исследований.
3. Электронно-вычислительные средства для расчетов.
4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).
5. Выводы.
6. Анализ и защита лабораторной работы производится по результатам представленного студентами отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы).
Преподаватель оценивает знание каждого студента.
Литература
