2015-10-16
301
Первообразная функция и неопределенный интеграл
Пусть функция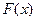 
определена и имеет производную
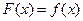
на некотором интервале. Тогда функция 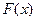называется первообразной для функции 
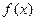на этом промежутке.
Пример.
Функция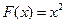 
является первообразной для функции 
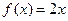на всей числовой оси, так для любого 
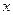выполняется 
.
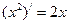Теорема. Пусть функция 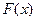является первообразной для функции 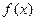. Тогда и функция
,
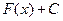в которой С – постоянная величина, также является первообразной для функции .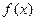
Обратно, есл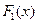и 
и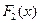 
- две различные первообразные для функции 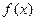, то они отличаются на постоянную величину С, т.е.
.
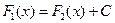Совокупность всех первообразных для функции 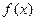называется неопределенным интегралом от функции 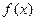в области определения первообразных.
Так как все первообразные для 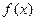отличаются друг от друга на постоянную величину, то ясно что
,
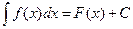т.е. неопределенный интеграл определяет семейство функций.
Процесс нахождения неопределенного интеграла от функции 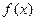называется интегрированием этой функции.
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной
функции
.
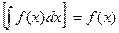2.Дифференциал от неопределенного интеграла равен подынтегральному выражению
.
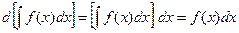3. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная
.
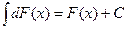4. Постоянный множитель можно вывести за знак интеграла
.
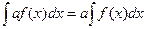5. Интеграл от алгебраической суммы конечного числа функций равен соответствующей алгебраической сумме интегралов от этих функций
.
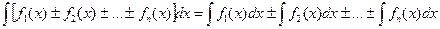Таблица неопределенных интегралов
1. 
.
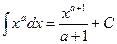
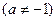2. 
.
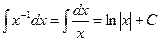3. 
.
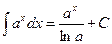4. 
.
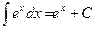5. 
.
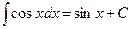6. 
.
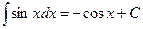7. 
.
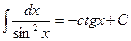8. 
.
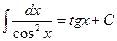9. 
.
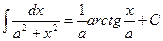10. 
.
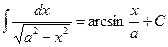11. 
.
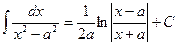12. 
.
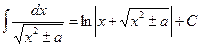Пример.
1. 
.
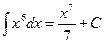2. 
.
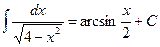Нахождение неопределенных интегралов путем обращения к таблице интегралов часто называют непосредственным интегрированием.
Методы вычисления неопределенных интегралов
Метод разложения
Пример.
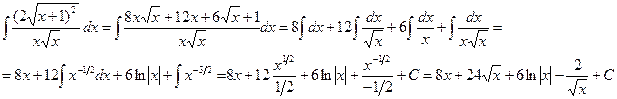
Пример.
.
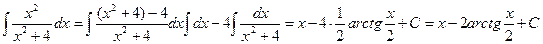Метод замены переменной
и легко находится выражение для интеграла через переменную интегрирования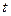 
. В заключении необходимо выполнить обратную подстановку, вернувшись к переменной .
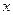Такая замена переменной позволяет свести сложный интеграл к табличному.
Пример. Рассмотрим последний пример, в котором использовалась подстановка
.
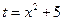Тогда
; 
; 
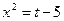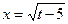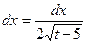
и, подставляя в исходный интеграл, имеем
.
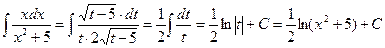Существует несколько типовых приемов при интегрировании методом замены переменной. Рассмотрим некоторые из них.
1. Если нужно найти интеграл от алгебраической дроби, причем в знаменателе дроби квадратный трехчлен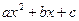 
, а в числителе – многочлен от 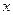не выше первой степени, то в знаменателе выделяется полный квадрат и новая переменная приравнивается к выражению, возводимому в квадрат.
Тот же прием применяется, если квадратный трехчлен находится под знаком квадратного корня.
Пример.
;
; 
 |
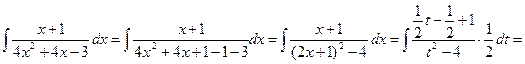
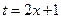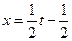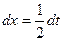
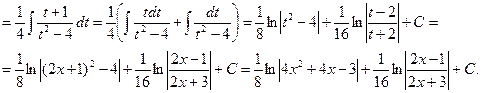
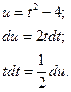
Интегрирование по частям
Формула интегрирования по частям
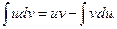
Интегрирование по частям обычно используют тогда, когда подынтегральная функция представляет собой произведение двух функций разного типа (степенной и тригонометрической; степенной и показательной; степенной и логарифмической; тригонометрической и показательной и т.п.).
Если в подынтегральном выражении имеется логарифмическая функция, то ее следует принять за u, а если логарифмической функции в подынтегральном выражении нет, то за u принимают степенную функцию. Все, что остается под интегралом, принимают за dυ.
Пример.
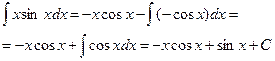
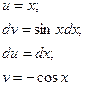
5. Рекомендуемое содержание отчета (для студента).
1. Название лабораторной работы.
2. Цель и задачи исследований.
3. Электронно-вычислительные средства для расчетов.
4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).
5. Выводы.
6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы).
Преподаватель оценивает знание каждого студента.
Литература
