а) Перевести 1101111001,1101(2) в восьмеричную систему счисления
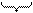 001 001
| 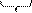 101 101
| 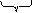 111 111
| 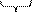 001 001
| , | 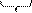 110 110
| 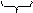 100 100
| = 1571,64(8) |
б) Перевести 11111111011,100111(2) в шестнадцатеричную систему счисления
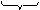 0111 0111
| 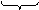 1111 1111
| 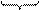 1011 1011
| , | 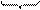 1001 1001
| 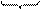 1100 1100
| = 7FB,9C(16) |
| F | B | С |
Перевод из восьмеричной в шестнадцатеричную систему и обратно удобно осуществлять через двоичную систему с помощью триад и тетрад.
Пример.
Перевести 175,24(8) в шестнадцатеричную систему счисления
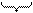 1 1
| 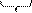 7 7
| 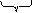 5 5
| , | 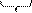 2 2
| 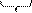 4 4
| (8) | 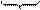 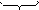 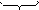 = 1111101,0101(2) = 0111 1101, 0101 (2) = 7D,5(16) = 1111101,0101(2) = 0111 1101, 0101 (2) = 7D,5(16)
|
| 7 D 5 |
Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами такие же, как и в десятичной системе, и задаются таблицами двоичного сложения, вычитания и умножения (таблица 2). Подобные таблицы для восьмеричной и шестнадцатеричной систем счисления приведены в Приложении.
Таблица 2 - Арифметические действия над двоичными числами
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0×0=0 0×1=0 1×0=0 1×1=1 |
При сложении двоичных чисел производится сложение цифр слагаемых в каждом разряде и единиц переноса из соседнего младшего разряда, если они имеются. При этом необходимо учитывать, что в двоичной системе переполнение разряда наступает при количестве единиц, больше либо равным двум. В случае переполнения нужно вычесть из текущего разряда число, равное основанию системы (в данном случае – два), и добавить единицу переноса в следующий старший разряд.
Прежде чем рассматривать приведенные ниже примеры, полезно попробовать получить для различных систем счисления порядковые последовательности путём прибавления единицы к предыдущему числу, начиная с нуля, а затем сравнить их с соответствующими столбцами таблицы 1. Затем попробуйте получить последовательности путём вычитания в обратном порядке.
 2015-10-13
2015-10-13 382
382








