Нормальное распределение задаётся интегральной функцией или плотностью распределения (дифференциальной функцией распределения) (рис. 13):
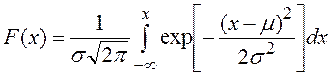 ;
;
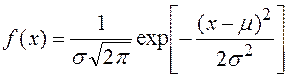 .
.
Для нормального распределения основные характеристики равны:
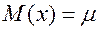 ,
, 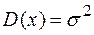 ,
, 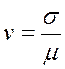 .
.
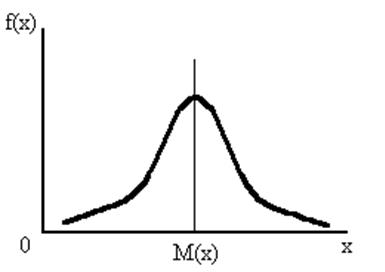
Рис. 13. Нормальное распределение случайной величины
Основные характеристики нормального распределения:
- математическое ожидание:
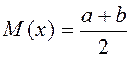 ,
,
- дисперсия:
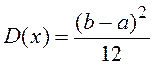 ,
,
- среднеквадратичное отклонение:
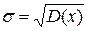
- коэффициент вариации:
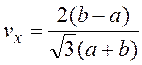 .
.
 2015-10-13
2015-10-13 403
403








