2015-10-13
549
Если система имеет нетиповую ЛАЧХ или является неминимально-фазовой, то строят непосредственно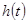 
, используя выражение (6-12). Однако непосредственные расчеты по нему весьма трудоемки. Идея упрощенного построения такова.
Характеристику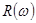 
, построенную в натуральном масштабе по оси частот, аппроксимируем стандартными характеристиками 
:
,
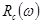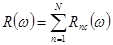тогда очевидно, что
,
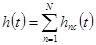где
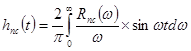(6-16)
В настоящее время чаще всего используют в качестве стандартных характеристик трапеции (рис. 6-8), при этом интеграл (6-16) может быть вычислен в виде
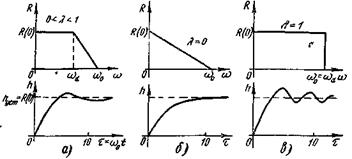
Рис 6-8
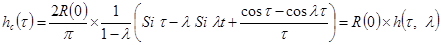(6-17)
где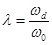 
— параметр трапеции, характеризующий ее форму 
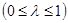(см. рис. 6-8, а, б, в);
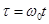— безразмерное время;
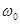— частота пропускания;
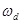— частота равномерного пропускания;
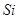— интегральный синус.
Функции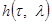 
в (6-17) табулированы (таблицы 
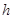-функций для трапеций имеются почти во всех книгах по теории автоматического регулирования, см., например. [1, 2, 3]).
Пример 6-3. Рассмотрим построение переходной функции САР, если ее ВЧХ имеет вид, показанный на рис. 6-9,а.
Аппроксимируя ее ломаной, получаем достаточно точное приближение с помощью трех трапеций (рис. 6-9,б),
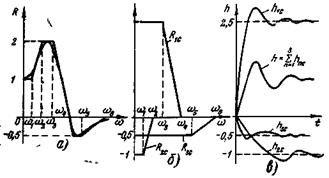
Рис. 6-9
для каждой из которых находится своя 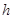-функция. Перейдя для каждой составляющей к натуральному времени
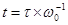, получаем 
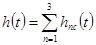(рис. 6-9,в),
