Преобразования координат Галилея

Исходные данные ______________________________________________________________________________

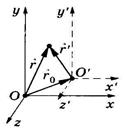Рассматривают две системы отсчета: инерциальную сис­тему отсчета К (с координатами х, у, z), условно считая ее неподвижной, и систему К' (с координатами х', у', z' ), движущуюся относительно К равномерно и прямоли­нейно со скоростью 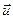( 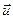= const). Отсчет времени — с мо­мента, когда начала координат обеих систем совпадают. На рисунке показано расположение систем в произволь­ный момент времени t. Скорость 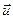направлена вдоль ОО'; .

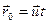Преобразования координат Галилея _____________________________________________________________

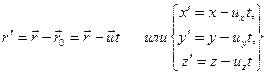Задают связь между радиусами-векторами или координатами произвольной точки Ав обеих системах.

Частный случай преобразований Галилея ________________________________________________________

Система К ' движется со скоростью 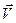вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают).

В классической механике считается, что ход времени не зависит от отно­сительного движения сиcтем отсчета, т. е. к преобразованиям Галилея добавляют уравнение t' = t.