Определение. Проективная система координат 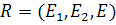 на расширенной евклидовой прямой
на расширенной евклидовой прямой 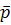 называется системой однородных координат, если одна из базисных точек (
называется системой однородных координат, если одна из базисных точек (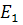 или
или 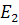 ) несобственная. Обычно полагают
) несобственная. Обычно полагают 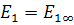 .
.
Замечание. Обычная система координат (афинных) на нерасширенной прямой p называется неоднородной. Она определяется двумя точками – началом координат 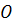 и точкой
и точкой 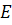 , координата которой равна единице.
, координата которой равна единице.
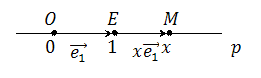
Если 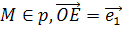 , то
, то 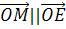 и
и 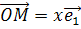 , где
, где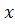 – действительное число.
– действительное число.
Таким образом, любая собственная точка 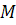 нерасширенной прямой
нерасширенной прямой 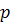 имеет определённую координату
имеет определённую координату 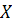 . В частности, точка
. В частности, точка 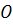 (начало координат) имеет нулевую координату. Координата несобственной точки неопределенна.
(начало координат) имеет нулевую координату. Координата несобственной точки неопределенна.
Преимущество однородной системы аффинных координат перед неоднородной состоит в том, что в однородной системе несобственная точка имеет определённые координаты. Как следует из примера 2 из §6 эти координаты равны 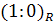 , так как точка
, так как точка 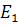 порождается вектором
порождается вектором 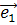 =
=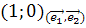 .
.
Координаты собственных точек расширенной евклидовой прямой 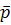 определяются следующеё теоремой.
определяются следующеё теоремой.
Теорема. Пусть на расширенной евклидовой прямой 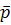 заданы:
заданы:
1. Неоднородная аффинная система координат 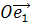 .
.
2. Однородная аффинная система координат 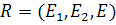 , где
, где 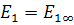 – несобственная точка,
– несобственная точка, 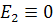 (
(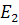 совпадает с 0),
совпадает с 0), 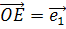 .
.
3. Произвольная собственная точка 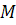 , имеющая в системе координат
, имеющая в системе координат 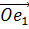 координату
координату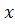 , а в системе координат
, а в системе координат 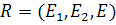 – координаты
– координаты 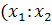 ).
).
Тогда: 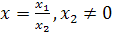 .
.
Доказательство:
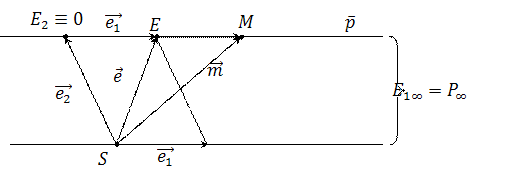
Точки 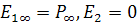 ,
, 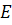 и
и 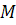 порождаются соответственно векторами
порождаются соответственно векторами 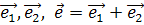 и
и 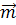 . Так как согласно замечанию
. Так как согласно замечанию 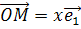 , то имеем:
, то имеем: 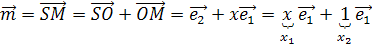 .
.
Отсюда 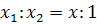 или окончательно
или окончательно 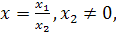 так как точка
так как точка 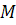 – собственная.
– собственная.
Теорема доказана.
Замечание. Несобственная точка 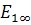 имеет координаты
имеет координаты 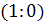 , то есть
, то есть 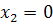 .
.
 2014-02-24
2014-02-24 1713
1713








