2015-10-13
484
Формулировки принципа относительности Галилея _______________________________________________
Законы динамики одинаковы во всех инерциальных системах отсчета.
Все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу.
Правило сложения скоростей в классической механике _______________________________________________
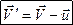Продифференцировав 
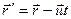по времени и учитывая, что t' = t 1.23,
получим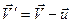 
.
[ 
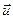— скорость движения системы К' относительно системы К 1.23; 
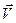и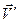 
— со ответственно скорости в системах К и К']
Подтверждение принципа относительности Галилея
(механического принципа относительности)_______________________________________________________
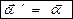В системе К ускорение 
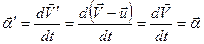. Следовательно, если на точку А другие тела не действуют (
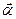= 0), то 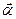а' = 0, т. е. система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).
Из равенства а' = а вытекает подтверждение принципа относительности Галилея (механического принципа относительности): уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.
е. являются инвариантными по отношению к преобразованиям координат.
Никакими механическими опытами, проводимыми внутри данной инерциальной системы отсчета, нельзя установить, покоится она или движется равномерно и прямолинейно. Во всех инерциальных системах отсчета одинаковы свойства пространства и времени, одинаковы и все законы механики.
