Потоки событий

Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например: поток вызовов на телефонной станции; поток отказов (сбоев) ЭВМ; поток железнодорожных составов, поступающих на сортировочную станцию; поток частиц, попадающих на счетчик Гейгера, и т. д.

Поток событий можно наглядно изобразить рядом точек на оси времени Ot (рис. 16.1); не надо только забывать, что положение каждой из них случайно, и на рис. 16.1 изображена только какая-то одна реализация потока

τ

------------------ · · · · · · · · · ·

О t

Рис. 16.1.

Говоря о «потоке событий», нужно иметь в виду, что здесь термин «событие» имеет значение, несколько отличное от того, к которому мы привыкли в теории вероятностей. Там «событием» (или «случайным со­бытием») называется какой-то исход опыта, обладающий той или другой вероятностью. События, образующие поток, сами по себе вероятностями не обладают; вероятностями обладают другие, производные от них события, например: «на участок времени т (рис. 16.1) попадет ровно два события», или «на участок времени At попадет хотя бы одно событие», или «промежуток времени между двумя соседними событиями будет не меньше t».

Важной характеристикой потока событий является его интенсивность λ — среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной (λ = const), так и переменной, зависящей от времени t. Например, поток автомашин, движущихся по улице, днем интенсивнее, чем ночью, в часы пик — интенсивнее, чем в другие часы.

Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени. На практике чаще встречаются потоки не регулярные, со случайными интервалами.

Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность X стационарного потока должна быть постоянной. Это отнюдь не значит, что фактическое число событий, появляющееся в единицу времени, постоянно,— нет, поток неизбежно (если только он не регулярный) имеет какие-то слу­чайные сгущения и разрежения, как, например, показано на рис. 16.1. Важно, что для стационарного потока эти сгущения и разрежения не носят законо­мерного характера: на один участок длины 1 может попасть больше, а на другой — меньше событий, но среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.

Одна из типичных ошибок начинающих — это принимать случайные сгущения и разрежения потока за изменения его интенсивности. Предостережем читателя от этой ошибки!

Как правило, отклонения от стационарности могут быть объяснены какими-то физическими причинами. Например, совершенно естественно, интенсивность потока вызовов, поступающих на АТС, ночью меньше, чем днем (ночью люди имеют обыкновение спать). Увеличение интенсивности потока покупателей, приходящих в магазин, в часы после окончания рабочего дня тоже имеет физическое объяснение. Если поток событий имеет тенденцию к явно выраженным сгущениям и разрежениям (особенно периодическим), нужно всегда заподозрить физическую причину и постараться ее выявить.

На практике часто встречаются потоки событий, которые (по крайней мере на ограниченном участке времени) могут считаться стационарными. Например, поток вызовов, поступающих на АТС между 13 и 14 часами, практически стационарен; тот же поток в течение суток уже не стационарен¹.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени т₁ и т₂ (см. рис. 16.2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути это означает, что события, образующие поток, появляются в те или другие моменты времени независимо друг от друга, вызванные каждое своими собственными причинами. Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток покупателей, отходящих от прилавка с купленными товарами, уже имеет последействие (хотя бы потому, что интервал по времени между

τ₁ τ₂

· · · · · · · · · · · ·

О t

Рис.16.2

отдельными покупателями не может быть меньше, чем минимальное время t₀ обслуживания каждого из них). Так же обстоит дело и с потоком поездов, подходящих к станции (между ними всегда существует какой-то минимальный интервал t₀, выбираемый из соображений безопасности).

Впрочем, если минимальный интервал между событиями много меньше среднего интервала между ними t = 1λ,, иногда наличием последействия можно пренебречь.

Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу. Например, поток клиентов, направляющихся в парикмахерскую или к зубному врачу, обычно ординарен, чего нельзя сказать о потоке клиентов, направляющихся в загс для регистрации брака. Поток поездов, подходящих к станции, ординарен, а поток вагонов — неординарен. Если поток событий ординарен, то вероятностью попадания на малый участок времени At двух или более событий можно пренебречь.

Заметим, что так же обстоит дело и с большинством процессов, которые в физике и технике мы называем «стационарными» — в действительности они стационарны лишь на ограниченном участке времени, а расширение его до бесконечности— только удобный прием.

Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последствия.'

Название «простейший» связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Между прочим, самый простой, на первый взгляд, регулярный поток не является «простейшим», так как обладает последействием: моменты появления событий в таком потоке связаны жесткой, функциональной зависимостью. Без специальных усилий по поддержанию его регулярности такой поток обычно не создается.

Простейший поток играет среди других потоков особую роль, в чем-то подобную роли нормального закона среди других законов распределения. А именно, при наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

Легко доказать (см., например, [12] или любой учебник по теории вероятностей), что для простейшего потока с интенсивностью X интервал Т между соседними событиями имеет так называемое показательное распределение с плотностью

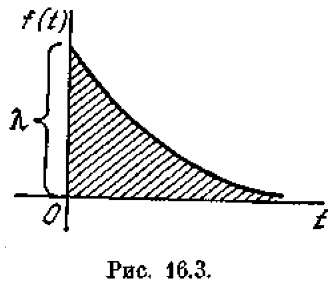
f(t) = λе^-λi (16.1)

(см. рис. 16.3). Величина X в формуле (16.1) называется параметром показательного закона. Для случайной величины Т, имеющей показательное распределение, математическое ожидание т_т есть величина, обратная параметру, а среднее квадратическое отклонение отравно математическому ожиданию:

m _τ = σ _τ = 1/λ. (16.2)

В теории вероятностей в качестве «меры случайно­сти» неотрицательной случайной величины нередко рассматривают так называемый коэффициент вариации:

V _т =σ_τ /m _т(16.3)

Из формул (16.2), (16.3) следует, что для показательного распределения v_T — 1, т. е. для простейшего потока событий коэффициент вариации интервалов между событиями равен единице.

Очевидно, что для регулярного потока событий, у которого интервал между событиями вообще не случаен (о_т = 0), коэффициент вариации равен нулю. Для большинства потоков событий, встречающихся на практике, коэффициент вариации интервалов между событиями заключен между нулем и единицей и может служить некоторой мерой «степени регулярности» потока: чем v_T ближе к нулю, тем «регулярнее» поток. Простейший поток — это «наименее регулярный» из встречающихся на практике потоков.

В расчетах, связанных с потоками событий, очень удобно пользоваться понятием «элемента вероятности». Рассмотрим на оси Ot простейший поток с интенсивностью Я и произвольно расположенный элементарный (очень маленький!) участок времени Δt. Элементом вероятности называется вероятность попадания на этот участок хотя бы одного события потока. Легко доказать (мы этого делать не будем), что элемент вероятности (с точностью до малых величин более высокого порядка по сравнению с Δt) равен

Р _Δt = λ Δt, (16.4)

т. е. для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка. Заметим, что элемент вероятности, в силу отсутствия последействия, совершенно не зависит от того, сколько событий и когда появлялись ранее.

Заметим также, что с точностью до величин высшего порядка малости вероятность появления хотя бы одного события на элементарном участке At равна вероятности появления ровно одного события на этом участке. Это вытекает из ординарности простейшего потока.

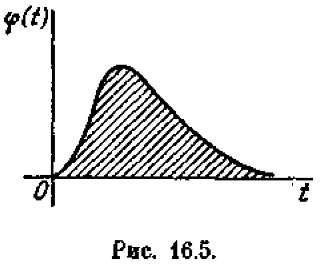
Поток событий называется рекуррентным (иначе— «потоком Пальма»), если он стационарен, ординарен, а интервалы времени между событиями Т₁, T₂, Т₃,... (см. рис. 16.4) представляют собой независимые случайные величины с одинаковым произвольным распределением (например, с плотностью, показанной на рис. 16.5). Приведем пример рекуррентного потока. Технический элемент (скажем, радиолампа) работает непрерывно до своего отказа (выхода из строя); отказавший элемент мгновенно заменяется новым. Если отдельные экземпляры элемента выходят из строя независимо друг от друга, то поток отказов (он же«поток замен» или «восстановлений») будет рекуррентным.

Рис. 16.4.

Другой пример. Продавец в магазине непрерывно занят обслуживанием покупателей (как это бывает в часы максимальной нагрузки). Обслуживание покупателя продолжается случайное время Т. Тогда поток обслуженных покупателей будет рекуррентным (если считать, что времена обслуживания отдельных покупателей независимы и, например, ссора между продавцом и покупателем не скажется на времени обслуживания других).

Очевидно, простейший поток представляет собой частный случай рекуррентного потока, когда интервалы между событиями имеют показательное распределение (16.1). Другим частным (вырожденным) случаем рекуррентного потока является регулярный поток событий, где интервалы вообще не случайны, постоянны.

Целую гамму рекуррентных потоков событий, обладающих разной степенью упорядоченности, можно получить «просеиванием» простейшего потока. Пусть, например, в какое-то учреждение поступает простейший поток посетителей, а у входа стоит «страж», направляющий первого посетителя — к первому столу, второго — ко второму столу и т. д. Если столов п, то на каждый из них поступает так называемый «поток Эрланга n-го порядка». Такой поток получается из простейшего, если сохранять в потоке каждое n -е событие, а промежуточные — выбрасывать. Простейший поток есть не что иное, как поток Эрланга первого порядка. Можно показать, что при таком просеивании простейшего потока коэффициент вариации интервалов уменьшается, и при увеличении порядка п поток Эрланга приближается к регулярному. Коэффициент вариации интервалов между событиями потока Эрланга n-го порядка равен v_T^(п) = 1/√ n. Потоки Эрланга образуют целую гамму потоков с различной степенью упорядоченности — от «полного беспорядка» (простейший поток) до полной упорядоченности (регулярный поток).