Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлений и т. д.). Если все потоки событий, переводящие систему S из состояния в состояние,— простейшие то процесс протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем «будущее» не зависит от «прошлого».
Если система S находится в каком-то состоянии Si, из которого есть непосредственный переход в другое состояние Sj(стрелка, ведущая из Si в Sjна графе состояний), то мы себе это будем представлять так, как будто на систему, пока она находится в состоянии Si действует простейший поток событий, переводящий се по стрелке Si → Sj. Как только появится первое событие этого потока, происходит «перескок» системы из Si в Sj.
Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим Δij интенсивность потока событий, переводящего систему из состояния Si в Sj-. На рис. 17.1 дан граф состояний с проставленными у стрелок интенсивностями (мы будем называть такой граф размеченным).
|
|
|
Построим размеченный граф состояний для примера, данного в § 15 (техническое устройство из двух узлов). Напомним состояния системы:
S0— оба узла исправны,
S1— первый узел ремонтируется, второй исправен,
S3— второй узел ремонтируется, первый исправен,
S4— оба узла ремонтируются.
1 Простейший характер потоков — достаточное, но не необходимое условие для того, чтобы процесс был марковским.
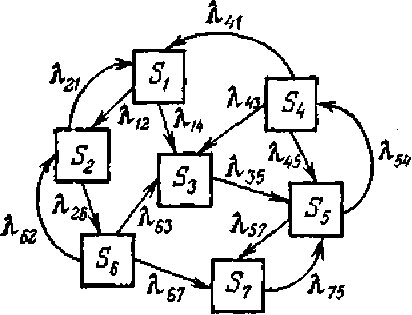 Рис. 17.1. Рис. 17.1. |
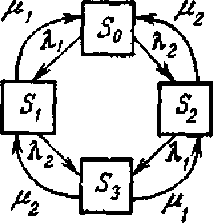 Рис. 17.2. Рис. 17.2. |
Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S0. Какой поток событий переводит ее в состояние Si? Очевидно, поток отказов первого узла. Его интенсивность λ1 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из S1 в S0? Очевидно, поток «окончаний ремонтов» первого узла. Его интенсивность μ1 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 17.2.
|
|
|
Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система S, имеющая п возможных состояний Sl, S2,..., Sn. Назовем вероятностью i-го состояния вероятность Pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
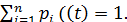 (І7.1)
(І7.1)
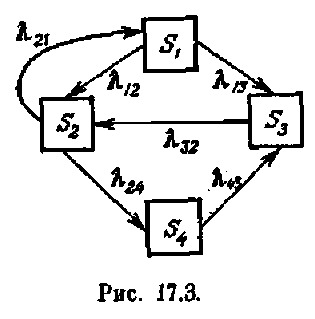 |
Покажем на конкретном примере, как эти уравнения составляются. Пусть система S имеет четыре состояния: S1 S2, S3, S4, размеченный граф которых показан на рис. 17.3. Рассмотрим одну из вероятностей состояний, например p1(t). Это — вероятность того, что в момент t система будет в состоянии Sl. Придадим t малое приращение Δt и найдем pl (t + Δt) — вероятность того, что в момент t + Δt система будет в состоянии Sl. Как это может произойти? Очевидно, двумя способами: либо 1) в момент t система уже была в состоянии Sl, а за время Δt не вышла из него; либо 2) в момент t система была в состоянии S2, а за время Δt перешла из него в Sl.
Найдем вероятность первого варианта. Вероятность того, что в момент t система была в состоянии Sl, равна pi(t). Эту вероятность нужно умножить на вероятность того, что, находившись в момент t в состоянии Sl, система за время Δt не перейдет из него ни в S2, ни в S3. Суммарный поток событий, выводящий систему из состояния Sl, тоже будет простейшим, с интенсивностью λ12 + λ13 (при наложении — суперпозиции — двух простейших потоков получается опять простейший поток, так как свойства стационарности, ординарyости и отсутствия последействия сохраняются). Значит, вероятность того, что за время Δt система выйдет из состояния Sit равна (Xi2 + X13)At; вероятность того, что не выйдет: 1 — (λ12 + λ13)Δt Отсюда вероятность первого варианта равна pi(t) [1 — (λi2 + λ13)Δt].
Найдем вероятность второго варианта. Она равна вероятности того, что в момент t система будет в состоянии S2, а за время Δt перейдет из него в состояние S1, т. е. она равна p2(t)λ21Δt.
Складывая вероятности обоих вариантов (по правилу сложения вероятностей), получим:
p1(t + Δt) = p1(t)[1 – (λ12 + λ13)Δt] + p2(t)λ21Δt.
Раскроем квадратные скобки, перенесем pi(t) в левую часть и разделим обе части на Δt:
р1 (t + Δt) – р1(t)/Δt= λ21р2(t) - (λ12 + λ13) р1 (t).
Устремим, как и полагается в подобных случаях, At к нулю; слева получим в пределе производную функции pi(t). Таким образом, запишем дифференциальное уравнение для pi(t):
dp1(t)/dt=λ21p2(t)-(λ12+λ13)p1(t),
или, короче, отбрасывая аргумент t у функций ph p2 (теперь он нам больше уже не нужен):
dp1/dt = λ21p2 – (λ21 + λ13) p1. + (17.2)
Рассуждая аналогично для всех остальных состояний, напишем еще три дифференциальных уравнения. Присоединяя к ним уравнение (17.2), получим систему дифференциальных уравнений для вероятностей состояний:
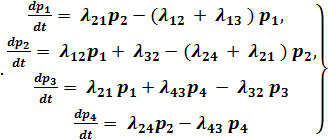 (17.3)
(17.3)
Это — система четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями pl, p2, p3, p4- Заметим, что одно из них (любое) можно отбросить, пользуясь тем, что pl + p2 + р3 + p4 = 1: выразить любую из вероятностей pi через другие, это выражение подставить в (17.3), а соответствующее уравнение с производной 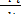 отбросить.
отбросить.
Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то (i -го) состояния. В правой части — сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i -го) состояния.
|
|
|
Пользуясь этим правилом, запишем уравнения Колмогорова для системы S, размеченный граф состояний которой дан на рис. 17.2:
 (17/4)
(17/4)
Чтобы решить уравнения Колмогорова и найти вероятности состояний, прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы Si, то в начальный момент (при t = 0) pi(0) = 1, а все остальные начальные вероятности равны нулю. Так, например, уравнения (17.4) естественно решать при начальных условиях р0(0) = 1, pl(0) = р2(0) = р3(0) = 0 (в начальный момент оба узла исправны).
Как решать подобные уравнения? Вообще говоря, линейные дифференциальные уравнения с постоянными коэффициентами можно решать аналитически, но это удобно только когда число уравнений не превос-
ходит двух (иногда — трех). Если уравнений больше, обычно их решают численно — вручную или на ЭВМ.
Таким образом, уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Поставим теперь вопрос: что будет происходить с вероятностями состояний при t →∞? Будут ли pi(t), p2(t),... стремиться к каким-то пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. В теории случайных процессов доказывается, что если число п состоя ний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют [2] .
Предположим, что это условие выполнено и финальные вероятности существуют:
lim p1(t) = p1 (i = 1,2,..., n). (17.5)
t→∞
Финальные вероятности мы будем обозначать теми же буквами р1, р2,..., что и сами вероятности состояний, но разумея под ними уже не переменные величины (функции времени), а постоянные числа. Очевидно, они тоже образуют в сумме единицу:
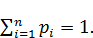 (17.6)
(17.6)
Как понимать эти финальные вероятности? При t →∞ да в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния Si можно истолковать как среднее относи тельное время пребывания системы в этом состоянии. Например, если система S имеет три состояния S1, S2, S3 и их финальные вероятности равны 0,2, 0,3 и 0,5, это значит, что в предельном, стационарном режиме система в среднем две десятых времени проводит в состоянии S1, три десятых — в состоянии S2 и половину времени — в состоянии S3.
|
|
|
Как же вычислить финальные вероятности? Очень просто. Если вероятности р1, р2,... постоянны, то их производные равны нулю. Значит, чтобы найти финальные вероятности, нужно все левые части в уравнениях Колмогорова положить равными нулю и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений. Можно и не писать уравнений Колмогорова, а прямо по графу состояний написать систему линейных алгебраических уравнений. Если перенести отрицательный член каждого уравнения из правой части в левую, то получим сразу систему уравнений, где слева стоит финальная вероятность данного состояния pi умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-e состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пользуясь этим правилом, напишем линейные алгебраические уравнения для финальных вероятностей состояний системы, граф состояний которой дан на рис, 17.2:
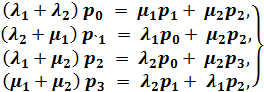 (17.7)
(17.7)
Эту систему четырех уравнений с четырьмя неизвестными ро, p1, p2, p3, казалось бы, вполне можно решить. Но вот беда: уравнения (17.7) однородны (не имеют свободного члена) и, значит, определяют неизвестные только с точностью до произвольного множителя. К счастью, мы можем воспользоваться так называемым нормировочным условием:
p0 + p1 + p2 + p3 = 1 (17.8)
и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
Давайте зададимся численными значениями интенсивностей λ1 = 1, λ2 = 2, μ1 = 2, μ2 = 3 и решим систему (17.7). Пожертвуем Четвертым уравнением, добавив вместо него нормировочное условие (17.8). Уравнения примут вид:
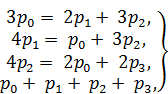 (17.9)
(17.9)
Решая их, получим: р0 = 6/15 = 0,40; р1 = 3/15 = 0,20; р2 = 4/15 ≈ 0,27; р3 = 2/15 ≈ 0,13, т. е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии S0 (оба узла исправны), 20% — в состоянии S1 (первый узел ремонтируется, второй работает), 27% —в состоянии S2 (второй узел ремонтируется, первый работает) и 13%—в состоянии S3 полной негодности (оба узла ремонтируются). Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов. Предположим, что система S в состоянии S0 (полностью исправная) приносит в единицу времени доход 8 (условных единиц), в состоянии S1 — доход 3, в состоянии S2 — доход 5, в состоянии S3 — вообще не приносит дохода. Тогда в предельном, стационарном режиме средний доход в единицу времени будет
W = 0,40 ∙ 8 + 0,20 • 3 + 0,27 • 5 - 5,15.
Теперь оценим загрузку ремонтных органов (рабочих), занятых ремонтом узлов 1 и 2. Узел 1 ремонтируется долю времени, равную р1 + p3 = 0,20 + 0,13 = 0,33. Узел 2 ремонтируется долю времени р2 + p3 = 0,40.
Здесь уже может возникнуть вопрос об оптимизации решения. Допустим, что мы можем уменьшить среднее время ремонта того или другого узла (может быть, и того, и другого), но это нам обойдется в какую-то сумму. Спрашивается, «стоит ли овчинка выделки»? Т. е. окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт?
Предоставим читателю самостоятельно поставить и решить такую экономическую задачу. При этом ему придется решать систему четырех уравнений с четырьмя неизвестными, но это ничего (характер, как известно, укрепляется в бедствиях!).
 2015-10-13
2015-10-13 14200
14200
