Задачи теории статистических решений

Близкой по идеям и методам к теории игр является теория статистических решений. От теории игр она отличается тем, что неопределенная ситуация не имеет конфликтной окраски — никто никому не противодействует, но элемент неопределенности налицо. В задачах теории статистических решений неизвестные условия операции зависят не от сознательно действующего «противника» (или других участников конфликта), а от объективной действительности, которую в теории статистических решений принято называть «природой». Соответствующие ситуации часто называются «играми с природой». «Природа» мыслится как некая незаинтересованная инстанция («равнодушная природа»,— по Пушкину),. «поведение» которой неизвестно, но во всяком случае не злонамеренно.

¹Изложенная здесь точка зрения автора на роль и значение теории игр вовсе не общепринята. Некоторые авторы, напротив, считают игровые подходы в исследовании операций основными (см., например, [28]).

Казалось бы, отсутствие сознательного противодействия упрощает задачу выбора решения. Оказывается, нет: не упрощает, а усложняет. Правда, принимающему решение в «игре с природой» в самом деле «легче» добиться успеха (ведь ему никто не мешает!), но ему «труднее» обосновать свой выбор. В игре против сознательного противника элемент неопределенности отчасти снимается тем, что мы «думаем» за противника, «принимаем» за него решение, самое неблагоприятное для нас самих. В игре же с природой такая концепция не подходит: кто ее знает, как она, матушка, себя поведет? Поэтому теория статистических решений — наиболее «шаткая» в смысле рекомендаций наука. Все же у нее есть право на существование и на -внимание со стороны лиц, занимающихся исследованием операций.

Рассмотрим игру с природой: у нас (сторона А) имеется т возможных стратегий А₁, А₂,,.., А_т; что касается обстановки, то о ней можно сделать п предположений: П₁ П₂,..., П_п. Рассмотрим их как «стратегии природы». Наш выигрыш а_и при каждой паре стратегий А_і, П, задан матрицей (таблица 28.1). Требуется выбрать такую стратегию игрока А (чистую или, может быть, смешанную, если это возможно), которая является более выгодной по сравнению с другими.

С первого взгляда кажется, что эта задача похожа на игру двух игроков А и П с противоположными интересами и должна решаться теми же методами. Но это не совсем так. Отсутствие противодействия со стороны природы делает ситуацию качественно другой¹.

Таблица 28.1

Пi А i	П1	П2	...	Пi
А1	а11	а12	...	а1n
А2	а21	а22	...	а2п
...	...	...	...	...
Ат	am1	ат2	...	атп

Давайте поразмышляем над задачей. Самый простой случай выбора решения в игре с природой — это случай когда (на наше счастье) какая-то из стратегий игрока А превосходит другие («доминирует» над ними), как, например, стратегия А₂ в таблице 28.2. Здесь выигрыш при стратегии А₂ при любом состоянии природы не меньше, чем при других стратегиях, а при некоторых — больше; значит, все ясно, и нужно выбирать именно эту стратегию.

¹К сожалению, нередки случаи, когда люди, малоискушенные в исследовании операций, встретившись на практике с такой ситуацией, забывают о «равнодушии» природы и сразу же начинают решать задачу методами теории антагонистических игр. Такие рекомендации встречаются и в книгах (преимущественно популярных).

Таблица 28.3

Пi А i	П1	П2	П3	П4
А1
A2
А3
А4

Если даже в матрице игры с природой нет одной доминирующей над всеми другими, все же полезно посмотреть, нет ли в ней дублирующих стратегий И уступающих другим при всех условиях (как мы это делали, упрощая матрицу игры). Но здесь есть одна тонкость: так мы можем уменьшить только число стратегий игрока А, но не игрока П — ему ведь все равно, много или мало мы выиграем! Предположим, что «чистка» матрицы произведена, и ни дублирующих, ни заведомо невыгодных игроку А стратегий в ней нет.

Чем же все-таки руководствоваться при выборе решения? Вполне естественно, должна учитываться матрица выигрышей (а_iЈ). Однако в каком-то смысле картина ситуации, которую дает матрица (а_iЈ), неполна и не отражает должным образом достоинств и недостатков каждого решения.

Поясним эту (далеко не простую) мысль. Предположим, что выигрыш а_iЈ при нашей стратегии A_i и состоянии природы П_Ј больше, чем при нашей стратегии A_k и состоянии природы П_Ј: а_iЈ>а_kЈ. Но за счет чего больше? За счет того, что мы удачно выбрали стратегию A_i? Необязательно. Может быть, просто состояние природы П_i выгоднее нам, чем П_Ј Например, состояние природы «нормальные условия» для любой операции выгоднее, чем «наводнение», «землетрясение» и т. п. Желательно ввести такие показатели, которые не просто давали бы выигрыш при данной стратегии в каждой ситуации, но отражали бы «удачность» или «неудачность» выбора данной стратегии в данной ситуации.

С этой целью в теории решений вводится понятие «риска». Риском r_iЈ - игрока А при пользовании стратегией А_i в условиях П_Ј называется разность между выигрышем, который мы получили бы, если бы знали условия П_Ј и выигрышем, который мы получим, не зная их и выбирая стратегию А_i.

Очевидно, если бы мы (игрок А) знали состояние природы П_Ј мы выбрали бы ту стратегию, при которой наш выигрыш максимален. Этот выигрыш, максимальный в столбце П_Ј мы уже раньше встречали и обозначили β_i Чтобы получить риск r_iЈ нужно из β_Ј вычесть фактический выигрыш а_iЈ:

Для примера возьмем матрицу выигрышей (я, (таблица 28.3) и построим для нее матрицу рисков (r_iЈ (таблица 28.4).

Таблица 28.3 Таблица28.4

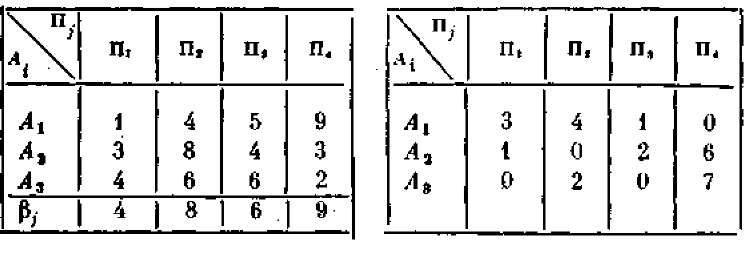
При взгляде на матрицу рисков (таблица 28.4) нам становятся яснее некоторые черты данной «игры с природой». Так, в матрице выигрышей (а_iЈ) (таблица 28.3) во второй строке первый и последний элементы были равны друг другу: а₂₁ = а₂₄ = 3. Однако эти выигрыши совсем не равноценны в смысле удачного вы­бора стратегии: при состоянии природы П₁ мы могли выиграть самое большее 4, и наш выбор стратегии А₂ почти совершенно хорош; а вот при состоянии П₄ мы могли бы, выбрав стратегию А₁, получить на целых 6 единиц больше, т. е. выбор стратегии А₂ очень плох. Риск — это «плата за отсутствие информации»: в таблице 28.4 r₂₁ = 1, r₂₄ = 6 (тогда как выигрыши а, в том и другом случае одинаковы). Естественно, нам хотелось бы минимизировать риск, сопровождающий выбор решения.

Итак, перед нами — две постановки задачи о выборе решения: при одной нам желательно получить максимальный выигрыш, при другой — минимальный риск.

Мы знаем, что самый простой случай неопределенности — это «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности Q₁, Q₂,..., Q_n и эти вероятности нам известны. Тогда естественно (со всеми оговорками, сделанными по этому поводу в § 5) выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально:

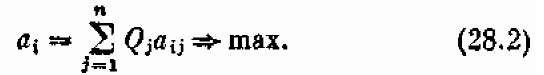
Любопытно отметить, что та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум и средний риск:

так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно И то же оптимальное решение.

Давайте чуточку «испортим» нашу неопределенность и допустим, что вероятности Q_i, Q₂,..., Q_n в принципе существуют, но нам неизвестны. Иногда в этом случае предполагают все состояния природы равновероятными (так называемый «принцип недостаточного основания» Лапласа), но вообще-то это делать не рекомендуется. Все- таки обычно более или менее ясно, какие состояния более, а какие — менее вероятны; Для того чтобы найти ориентировочные значения вероятностей Q_i, Q₂,..., Q_n, можно, например, воспользоваться методом экспертных оценок (см. § 5). Хоть какие-то ориентировочные значения вероятностей состояний природы все же лучше, чем полная неизвестность. Неточные значения вероятностей состояний природы в дальнейшем могут быть «скорректированы» с помощью специально поставленного эксперимента. Эксперимент может быть как «идеальным», полностью выясняющим состояние природы, так и неидеальным, где вероятности состояний уточняются по косвенным данным. Каждый эксперимент, разумеется, требует каких-то затрат, и возникает вопрос: окупаются ли эти затраты возрастанием эффективности?

Оказывается, «идеальный» эксперимент имеет смысл проводить только в случае, когда его стоимость меньше, чем минимальный средний риск (см., например, [6]).

Однако не будем больше заниматься случаем стохастической неопределенности, а возьмем случай «дурной неопределенности», когда вероятности состоянии" природы либо вообще не существуют, либо не поддаются оценке даже приближенно. Ну что же?.Обстановка неблагоприятна для принятия «хорошего» решения— попытаемся найти хотя бы не самое худшее.

Здесь все зависит от точки зрения на ситуацию, от позиции исследователя, от того, какими бедами грозит неудачный выбор решения, Опишем несколько возможных подходов, точек зрения (или, как говорят, несколько «критериев» для выбора решения).

1. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разум ным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оп тимальной считается стратегия, при которой гаранти руется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой»:

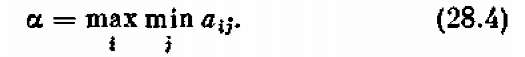
Если руководствоваться этим критерием, олицетво­ряющим «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Очевидно, такой подход — «перестраховочный», естественный для того, кто очень боится проиграть,— не является единственно возможным, но как крайний случай он заслуживает рассмотрения.

2. Критерий минимаксного риска Сэвиджа. Этот критерий — тоже крайне пессимистический, но при вы боре оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оп тимальной та стратегия, при которой величина риска в наихудших условиях минимальна:

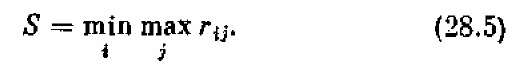
Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.

3. Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руко водствоваться ни крайним пессимизмом («всегда рас считывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Согласно этому критерию выбирается стратегия из условия

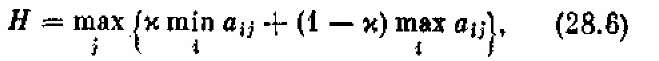
где х — «коэффициент пессимизма», выбираемый между нулем и единицей. При х = 1 критерий Гурвица превращается в критерий Вальда; при х = 0 — в критерий «крайнего оптимизма», рекомендующий выбрать ту стратегию, при которой самый большой выигрыш в строке максимален. При 0 < х < 1 получается нечто среднее между тем и другим. Коэффициент х выбирается из субъективных соображений — чем опаснее ситуация, чем больше мы хотим в ней «подстраховаться», чем менее наша склонность к риску, тем ближе к единице выбирается х.

При желании можно построить критерий, анало­гичный Н, исходя не из выигрыша, а из риска, но мы на этом не будем останавливаться.

«Что же,— спросит читатель,— выбор критерия — субъективен, выбор коэффициента х — тоже субъективен, значит и решение тоже принимается субъективно, т. е., грубо говоря, произвольно? Где же тут наука? При чем тут математика? Может быть, лучше было бы просто, без математических затей, выбрать решение по своему произволу?»

В какой-то мере читатель прав — выбор решения в условиях неопределенности всегда условен, субъективен. И все же в какой-то (ограниченной) мере математические методы полезны и тут. Прежде всего, они позволяют привести игру с природой к матричной форме, что далеко не всегда бывает просто, особенно когда стратегий много (в наших примерах их было очень мало). Кроме того, они позволяют заменить простое лицезрение матрицы выигрышей (или рисков), от которого, когда матрица велика, может просто «зарябить в глазах», последовательным численным анализом ситуации с разных точек зрения, выслушать рекомендации каждой из них и, наконец, остановиться на чем-то определенном. Это аналогично обсуждению вопроса с различных позиций, а в споре, как известно, рождается истина. Так что не ждите от теории решений окончательных, непререкаемых рекомендаций — единственное, чем она может помочь — это советом...

Если рекомендации, вытекающие из различных критериев, совпадают — тем лучше, значит, можно смело выбрать рекомендуемое решение: оно скорее всего «не подведет». Если же, как это часто бывает, рекомендации противоречат друг другу, не надо забывать, что у нас голова на плечах. Задумаемся над этими рекомендациями, выясним, насколько к разным ре­зультатам они приводят, уточним свою точку зрения и произведем окончательный выбор. Не надо забывать, что в любых задачах обоснования решений некоторый произвол неизбежен — хо тя бы при построении ма­тематической модели, выборе показателя эффективности. Вся математика, применяемая в исследовании операций, не отменяет этого произвола, а позволяет только «поставить его на свое место».

Таблица 28.5 ПЈ Аi П1 П2 П3 А1       А2       А3       A4

Рассмотрим элементарный пример «игры с природой» 4 X 3, матрица выигрышей которой (а) дана в таблице 28.5. Поглядим на матрицу и попробуем сразу, без расчетов, указать, какой стратегией пользоваться? Несмотря на малый размер матрицы, это не так-то легко.

Теперь попробуем помочь себе, пользуясь критериями Вальда, Сэвиджа и Гурвица, причем в последнем возьмем х = 0,6 (перевес чуть-чуть в сторону пессимизма). Что-то они нам скажут?

1. Слово имеет критерий Вальда. Подсчитаем минимумы по строкам (см. таблицу 28.6) и выберем ту стратегию, при которой минимум строки максимален (равен 25). Это — стратегия А₃.

Таблица 28.6

ПЈ Аi	П1	П2	П3	αi
А1
А2
А3
А4

2. Слово имеет критерий Сэвиджа. Перейдем от матрицы выигрышей (таблица 28.6) к матрице рисков (таблица 28.7), в правом дополнительном столбце запишем максимальное в строке значение риска у_г-.

Из чисел правого столбца минимальное (60) соответствует стратегиям А₂ и А₂; значит, обе они оптимальны по Сэвиджу.

Таблица 28.7

ПЈ Аi	П1	П2	П3	υi
А1
A2				60
А3
А4

3. Слово имеет критерий Гурвица (при х = 0,6). Опять перепишем таблицу 28.5, но на этот раз в правых трех дополнительных столбцах поставим: минимум строки a_i ее максимум ω_і и величину h_i = χα_i + (1 — χ) хω_і, округленную до целых единиц (см. таблицу 28.8).

Максимальное значение h_ί = 47 соответствует стратегии А ₃.

Итак, в данном случае все три критерия согласно говорят в пользу стратегии А₃, которую есть все основания выбрать.

Таблица 28.8

ПЈ Аi	П1	П2	П3	αi	ωі	υі
A1
Аг
A3
A4

А теперь возьмем случай, когда между критериями возникает «спор». Матрица выигрышей (аίЈ) (с заранее выписанными столбцами минимумов строк а_ίЈ максимумами строк и значениями h_l (при χ ⁼ 0,6) дана в таблице 28.9.

По критерию Вальда оптимальной является стратегия Aj, по критерию Гурвица с χ = 0,6 — стратегия А₃. Посмотрим, что скажет критерий Сэвиджа. Матрица рисков с дополнительным столбцом, содержащим максимумы строк у_г-, дана в таблице 28.10.

Таблица 28.9

ПЈ Аi	П1	П2	П3	П4	αi	ωi	hi
А1
A2
А3

Минимальным в последнем столбце является число 38, так что критерий Сэвиджа, так же как и критерий Гурвица, «голосует» за стратегию А ₃.

Над этим стоит поразмыслить. Если мы очень боимся малого выигрыша «11», который нас может постигнуть при стратегии А₃, ну что же — выберем стратегию A_jЈ рекомендуемую крайне осторожным критерием Вальда, при котором мы, по крайней мере, можем себе гарантировать выигрыш «19», а может быть, и больше. Если же наш пессимизм не так уж мрачен, пожалуй, надо остановиться на стратегии А₃, рекомендуемой двумя из трех критериев.

Таблица 28.10

ПЈ Аi	П1	П2	П3	П4	vi
А1
А2
А3

Читатель, конечно заметил, что тут мы говорим на каком-то нематематическом языке, а скорее на языке

«рассуждений и здравого смысла». Что поделаешь — в неопределенности ничего хорошего нет, и при отсутствии нужной информации никакая математика не поможет нам в однозначном выборе «оптимального» решения. Жизнь есть жизнь, будущее полно неопределенностей, и нам зачастую приходится принимать отнюдь не строго оптимальные, а «приемлемые» решения, при обсуждении которых разные «подходы» и «критерии» выступают в качестве как бы спорящих сторон.

В заключение отметим следующее: все три критерия (Вальда, Сэвиджа и Гурвица) были сформулированы нами для чистых стратегий, но каждый из них может быть распространен и на смешанные, подобно тому, как мы это делали в теории игр. Однако смешанные стратегии в игре с природой имеют лишь ограниченное (главным образом, теоретическое) значение. Если в игре против сознательного противника смешанные стратегии иногда имеют смысл как «трюк», вводящий в заблуждение противника, то в игре против «равнодушной природы» этот резон отпадает. Кроме того, смешанные стратегии приобретают смысл только при многократном повторении игры. А если уж мы ее повторяем, то неизбежно начинают вырисовываться какие-то вероятностные черты ситуации, и мы ими можем воспользоваться для того, чтобы применить «стохастический подход» к задаче, а он, как мы знаем, смешанных стратегий не дает. Кроме того, в ситуациях с «дурной» неопределенностью, когда нам мучительно не хватает информации, главная задача — эту информацию получить, а не выдумывать хитроумные методы, позволяющие без нее обойтись. Одна из основных задач теории статистических решений — это как раз планирование эксперимента, цель которого — выяснение или уточнение каких-то данных. На вопросах планирования эксперимента мы здесь останавливаться не будем: это отдельный предмет, требующий серьезного внимания. По этому вопросу мы отошлем читателя к специальным руководствам [29, 30], а также к интересно написанной популярной книге [27]. Основной принцип теории планирования эксперимента состоит в том, что любое принятое заранее решение должно пересматриваться с учетом полученной новой информации.

Таким образом, наш краткий обзор, посвященный задачам, принципам и методологии исследования операций, закончен. В нем автор стремился ознакомить читателя не только с возможностями, но и с ограничениями математических методов, применяемых для обоснования решений. Главное — ни один из этих методов не избавляет человека от необходимости думать. Но не просто думать, а пользоваться при этом математическими расчетами. Помня, что, по меткому выражению Хемминга,— «главная цель расчетов — не цифры, а понимание».

ЛИТЕРАТУРА

С а а т и Т. Л. Математические методы исследования операций.— М.: Воениздат, 1963 (около 25 п. л.).

Вентцель Е. С. Теория вероятностей (первые шаги).— М.: Знание, 1977 (около 3,5 п. л.).

Подиновский В. В., Гаврилов В. М. Оптимизация по последовательно применяемым критериям.— М.: Советское радио, 1975 (около 8 п. л.).

Карпелевич Ф. И., Садовский Л. Е. Элементы линейной алгебры и линейного программирования.— М.: Наука, 1967 (около 15 п. л.).

Ю д и н Д. В., Г о л ь ш т е й н Е. Г. Линейное программирование.— М.: Наука, 1967 (около 40 п. л.).

Вентцель Е. С. Исследование операций.— М.: Советское радио, 1972 (около 35 п. л.).

В а г н е р Г. Основы исследования операций.— М.: Мир, 1972 (в трех томах, общий объем около 80 п. л.).

3 у х о в и ц к и й С. И.,Авдеева Л. И. Линейное и выпуклое программирование.— М.: Наука,1964 (около 17 п. л.).

9 Г у р и н Л. С, Д ы м а р с к и й Я. С, Меркулов А. Д. Задачи и методы оптимального распределения ресурсов.— М.: Советское радио, 1968 (около 25 п. л.).

Беллман Р. Динамическое программирование.—М.: Иностранная литература, 1960 (около 25 п. л.).

Вентцель Е. С. Элементы динамического программирования.— М.: Наука, 1964 (около 10 п. л.).

В е н т ц е л ь Е. С. Теория вероятностей.— М.: Наука, 1964 (около 35 п. л.).

Розенберг В. Я., Прохоров А. И. Что такое теория массового обслуживания.— М.: Советское радио, 1962 (около 13 п. л.).

О в ч а р о в Л. А. Прикладные задачи теории массового обслуживания.—М.: Машиностроение, 1969 (около 18 п. л.).

Кофман А., Крюон Р. Массовое обслуживание, теория и применения,—М.: Прогресс, 1965 (около 20 п. л.).

Г н е д е н к о Б. В., Коваленко И. Н. Введение в теорию массового обслуживания.— М.: Наука, 1966 (около 22 п. л.).

С а а т и Т. Л. Элементы теории массового обслуживания и ее приложения.— М.: Советское радио, 1971 (около 32 п. л.).

Платонов Г. А., Файнберг М. А., Штильм а н М. С. Поезда, пассажиры и... математика.— М.: Транспорт, 1977 (около 10 п. л.).

С е в а с т ь я н о в В. А. Формулы Эрланга в телефонии.— Труды III математического съезда, т. IV, изд. АН СССР, 1959.

Гмурман В. Е. Теория вероятностей и математическая статистика.—М.: Высшая школа, 1977 (около 22 п. л.).

Вентцель Е. С. Исследование операций.— М.: Знание, 1976 (около 3,5 п. л.).

Соболь И. М. Метод Монте-Карло.—М.: Физматгиз, 1968 (около 3,5 п. л.).

Исследование операций (методологические аспекты).—. М.: Наука, 1972 (около 4 п. л).

Вентцель Е. С. Элементы теории игр.— М.: Физматгиз, 1969 (около 4 п. л.).

М а к - К и н с и Дж. Введение в теорию игр.— М.: Физматгиз, 1960 (около 20 н. л.).

Л ь ю с Р. Д., Р а й ф а X. Игры и решения.— М.: Иностранная литература, 1961 (около 40 п. л.).

X у р г и н Я. И. Да, нет или может быть...—М.: Наука, 1977 (около 10 п л.).

Г е р ме й е р Ю. Б. Введение в теорию исследования операций —М.: Наука, 1971 (около 20 п. л.).

Налимов В. В. Теория эксперимента.— М.: Наука, 1971 (около 10 п. л.).

В а л ь д А. Последовательный анализ,— М.: Физматгиз, 1960 (около 17 п. л.).

Юдин Д. Б. Математические методы управления в условиях неполной информации.— М.: Советское радио, 1974 (около 30 п. л.).

предметный указатель

Алгоритм адаптивный 37

Величина случайная 31

Граф состояний 117

— размеченный 125

Игра 175

—антагонистическая 177

—биматричная 193

—деловая 25

—конечная(бесконечная) 176

—парная (множественная) 175

—с нулевой суммой 177

—с полной информацией 182

—с природой 195

—стратегическая 176

Канал обслуживания 132

Критерий аддитивный 85

—максиминный Вальда.200 —минимаксного риска Сэвиджа 200

— мультипликативный 111

— пессимизма-оптимизма Гурвица 200

Максимин 180

Метод игровой обоснования решений 173

— итераций Брауна — Робинсон 190

— Монте-Карло 24, 161

— последовательных уступок 49

— потенциалов 78

— штрафных функций 82

— эвристический 48

— экспертных оценок 41

Минимакс 180

Моделирование «имитационное» 25

— статистическое 24, 161 и д.

Неопределенность стохастическая 32

Ограничения стохастические 35

Оптимизация в среднем 34

Пара двойственных задач линейного программирования 189

Перебор направленный, простой

План оптимальный 73

Планирование эксперимента 205

Поиск случайный 83

Показатель эффективности 17,44, 45 Поток заявок 132

Поток событий 117—124

Принцип гарантированного результата 39

— минимакса 179

— недостаточного основания Лапласа 199

— оптимальности 107

— Программирование динамическое 84

— линейное 28. 52

— математическое 52

— нелинейное 80

— стохастическое 83

— целочисленное 80

Режим диалоговый 49

Решение игры 181

— опорное 69

— оптимальное 15 63

— «паретовское» 47

— Риск 197

Система сложная 50

— массового обслуживания

(СМО) 132 и д.

Ситуация конфликтная 174

Стратегия доминирующая 196

— дублирующая 185

— минимаксная 180

— оптимальная чистая 176, 181

— смешанная 182

Таблица случайных чисел 169

Теорема основная теории игр 184

Управление оптимальное 85,91,

— шаговое 85

— Уравнения Колмогорова 124

— Условие нормировочное 130 Устойчивость статистическая 37

Формула Литтла 140

(формулы Полячека—Хинчина

— Эрланга 144

— Функционал 28

— Функция случайная 31

— целевая 17

— Ход 175

Цена игры 180—181

Число случайное, псевдослучайное 169

Элемент вероятности 123

— решения 16

¹ В случае, если читатель вовсе незнаком с теорией веро­ятностей, минимально необходимые сведения он может получить из популярной брошюры [2].

Термин «стохастический» попросту значит «вероятност­ный», но звучит как-то торжественней. Сохраняем здесь этот термин, так как он употребителен в литературе.

¹ Более подробно о различных подходах к выбору реше­ния в условиях неопределенности сказано в главе 8.

¹ К сожалению, этим недостатком страдает и книга [6] автора, где ряд выводов получен недостаточно просто.

В сущности, вся методика практического применения теории вероятностей основана на том, что маловероятные события мы попросту считаем невозможными (об этом, а также о принципах назначения «уровня доверия» см. [2])

^[2] Это условие достаточно, но не необходимо для существования финальных вероятностей

^[3] В популярной книжке [18] дан несколько иной, по сравнению с вышеизложенным- вывод формулы Литтла Вообще, знакомство с этой книжкой («Беседа вторая») полезно для первоначального' ознакомления с теорией массового обслуживания.

^[4] Точнее, обладают одинаковой плотностью вероятности.