Критические области

Статистическую гипотезу проверяют с помощью специально подобранной случайной величины, точное или приближенное распределение которой известно (обозначим ее К). Эту случайную величину называют статистическим критерием (или просто критерием).

Существуют различные статистические критерии, применяемые на практике: U- и Z -критерии (эти случайные величины имеют нормальное распределение); F -критерий (случайная величина распределена по закону Фишера - Снедекора); t -критерий (по закону Стьюдента); 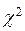-критерий (по закону "хи-квадрат") и др.

Множество всех возможных значений критерия можно разбить на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза принимается, а другое - при которых она отвергается.

Множество значений критерия, при которых нулевая гипотеза отвергается, называется критической областью. Будем обозначать критическую область через W.

Множество значений критерия, при которых нулевая гипотеза принимается, называется областью принятия гипотезы (или областью допустимых значений критерия). Будем обозначать эту область как .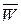

Для проверки справедливости нулевой гипотезы по данным выборок вычисляют наблюдаемое значение критерия. Будем обозначать его К _набл.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия попало в критическую область (то есть 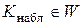), то нулевую гипотезу отвергают; если же наблюдаемое значение критерия попало в область принятия гипотезы (то есть 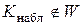), то нет оснований отвергать нулевую гипотезу.

Какими принципами следует руководствоваться при построении критической области W?

Допустим, что гипотеза Н₀ на самом деле верна. Тогда попадание критерия 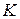в критическую область в силу основного принципа проверки статистических гипотез влечет за собой отклонение верной гипотезы Н₀, а значит, совершение ошибки первого рода. Поэтому вероятность попадания 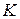в область W при справедливости гипотезы Н₀ должна быть равна уровню значимости критерия, то есть

.

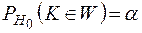Заметим, что вероятность совершить ошибку первого рода выбирается достаточно малой (как правило, 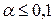). Тогда попадание критерия 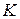в критическую область W при справедливости гипотезы Н₀ можно считать практически невозможным событием. Если по данным выборочного наблюдения событие 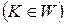все же наступило, то его можно считать несовместимым с гипотезой Н₀ (которая в результате и отвергается), но совместимым с гипотезой Н₁ (которая в результате принимается).

Предположим теперь, что верна гипотеза Н₁. Тогда попадание критерия 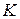в область принятия гипотезы 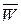влечет за собой принятие неверной гипотезы Н₀, что означает совершение ошибки второго рода. Поэтому .

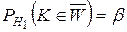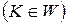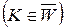Так как события и являются взаимно противоположными, то вероятность попадания критерия 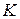в критическую область W будет равна мощности критерия, если гипотеза Н₁ верна, то есть

.

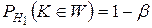Очевидно, что критическую область следует выбирать так, чтобы при заданном уровне значимости 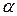мощность критерия 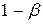была максимальной. Максимизация мощности критерия обеспечит минимум вероятности допустить ошибку второго рода.

Следует отметить, что как бы ни было мало значение уровня значимости 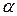, попадание критерия в критическую область есть только маловероятное, но не абсолютно невозможное событие. Поэтому не исключено, что при верной нулевой гипотезе значение критерия, вычисленное по данным выборки, все же окажется в критической области. Отклоняя в этом случае гипотезу Н₀, мы допускаем ошибку первого рода с вероятностью 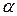. Чем меньше 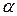, тем менее вероятно допустить ошибку первого рода. Однако с уменьшением 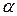уменьшается критическая область, а значит, становится менее возможным попадание в нее наблюдаемого значения К _набл, даже когда гипотеза Н₀ неверна. При 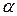=0 гипотеза Н₀ всегда будет приниматься независимо от результатов выборки. Поэтому уменьшение 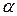влечет за собой увеличение вероятности 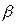принять неверную нулевую гипотезу, то есть совершить ошибку второго рода. В этом смысле ошибки первого и второго рода являются конкурирующими.

Так как исключить ошибки первого и второго рода невозможно, необходимо хотя бы стремиться в каждом конкретном случае свести к минимуму потери от этих ошибок. Конечно, желательно уменьшить обе ошибки одновременно, но так как они являются конкурирующими, то уменьшение вероятности допустить одну из них влечет увеличение вероятности допустить другую. Единственный путь одновременного уменьшения риска ошибок заключается в увеличении объема выборки.

В зависимости от вида конкурирующей гипотезы Н₁ строят одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области. Точки, отделяющие критическую область 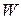от области принятия гипотезы 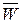, называют критическими точками и обозначают k _крит. Для отыскания критической области необходимо знать критические точки.

Правосторонняя критическая область может быть описана неравенством 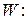К > k _{крит. пр}, где предполагается, что правая критическая точка k _{крит. пр}>0. Такая область состоит из точек, находящихся по правую сторону от критической точки k _{крит. пр}, то есть она содержит множество положительных и достаточно больших значений критерия К. Для нахождения k _{крит. пр} задают сначала уровень значимости критерия 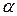. Далее правую критическую точку k _{крит. пр} находят из условия 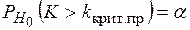. Почему именно это требование определяет правостороннюю критическую область? Так как вероятность события (К > k _{крит. пр} ) мала, то, в силу принципа практической невозможности маловероятных событий, это событие при справедливости нулевой гипотезы в единичном испытании не должно наступить. Если все же оно наступило, то есть вычисленное по данным выборок наблюдаемое значение критерия 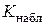оказалось больше k _{крит. пр}, то это можно объяснить тем, что нулевая гипотеза не согласуется с данными наблюдения и поэтому должна быть отвергнута. Таким образом, требование 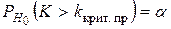определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они и составляют правостороннюю критическую область.

Если же 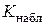попало в область допустимых значений критерия , то есть 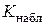< k _{крит. пр}, то основная гипотеза не отвергается, ибо она совместима с данными наблюдения. Заметим, что вероятность попадания критерия 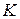в область допустимых значений 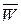при справедливости нулевой гипотезы равна (1- 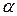) и близка к 1.

Необходимо помнить, что попадание значений критерия 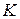в область допустимых значений не является строгим доказательством справедливости нулевой гипотезы. Оно лишь указывает, что между выдвигаемой гипотезой и результатами выборки нет существенного расхождения. Поэтому в таких случаях говорят, что данные наблюдений согласуются с нулевой гипотезой и нет оснований отвергать ее.

Аналогично проводится построение и других критических областей.

Так, левосторонняя критическая область описывается неравенством 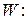К < k _{крит. л}, где k _крит.л<0. Такая область состоит из точек, находящихся по левую сторону от левой критической точки k _крит.л, то есть она представляет собой множество отрицательных, но достаточно больших по модулю значений критерия. Критическую точку k _крит.л находят из условия 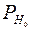(К < k _{крит. л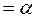}) , то есть вероятность того, что критерий принимает значение, меньшее k _крит.л, равна принятому уровню значимости 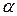, если нулевая гипотеза верна.

Двусторонняя критическая область 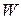описывается следующими неравенствами: (К<k _крит.л или К > k _{крит. пр}), где предполагается, что k _крит.л<0 и k _{крит. пр}>0. Такая область представляет собой множество достаточно больших по модулю значений критерия. Критические точки находят из требования: сумма вероятностей того, что критерий примет значение, меньшее k _{крит. л} или больше k _{крит. пр}, должна быть равна принятому уровню значимости при справедливости нулевой гипотезы, то есть

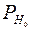(К<k _{крит. л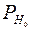} )+ (К > k _{крит. пр} )= .

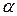Если распределение критерия К симметрично относительно начала координат, то критические точки будут располагаться симметрично относительно нуля, поэтому k _{крит. л} = - k _{крит. пр}. Тогда двусторонняя критическая область становится симметричной и может быть описана следующим неравенством: 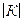>k _{крит. дв}, где k _{крит. дв} = k _{крит. пр} Критическую точку k _{крит. дв} можно найти из условия

Р(К< - k _{крит. дв} )=Р(К > k _{крит. дв} )= .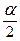

Замечание 1. Для каждого критерия К критические точки при заданном уровне значимости 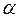могут быть найдены из условия 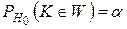только численно. Результаты численных вычислений k _крит приведены в соответствующих таблицах (см., например, прил. 4 – 6 в файле «Приложения»).

Замечание 2. Описанный выше принцип проверки статистической гипотезы не доказывает еще ее истинность или неистинность. Принятие гипотезы Н₀ в сравнениис альтернативной гипотезой Н₁ не означает, что мы уверены в абсолютной правильности гипотезы Н₀ - просто гипотеза Н₀ согласуется с имеющимися у нас данными наблюдения, то есть является достаточно правдоподобным, не противоречащим опыту утверждением. Возможно, что с увеличением объема выборки n гипотеза Н₀ будет отвергнута.