2015-10-13
3506
На практике изменение результативного признака y зачастую зависит от действия нескольких факторных признаков x, поэтому изучение связи между тремя признаками и более носит название множественной (многофакторной) регрессии. Аналитическое выражение связи между результативным признаком y и факторными признаками (x 1, x 2, …, xk) описывается функцией вида
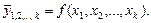
Уравнение множественной регрессии описывает математическую зависимость результативного признака от нескольких факторных признаков.
При построении уравнения множественной регрессии необходимо решить следующие задачи:
· обосновать взаимосвязь результативного признака и факторных признаков;
· определить тип уравнения регрессии;
· количественно оценить тесноту связи между результативным признаком и факторами.
Построение моделей множественной регрессии включает три этапа:
1) выбор формы связи (уравнения регрессии);
2) отбор факторных признаков;
3) обеспечение достаточного объема совокупности.
Выбрать тип уравнения довольно сложно, так как любой форме связи могут соответствовать несколько уравнений, описывающих эти связи.
Проблема отбора факторных признаков может быть решена на основе интуитивно-логических или многомерных математико-статистических методов. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия. Она заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Если при включении нового фактора в уравнение коэффициенты регрессии меняют свои значения и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак не рекомендуется включать в уравнение связи.
Многофакторные регрессионные модели делятся на линейные (относительно независимых переменных) и нелинейные.
Наиболее простым для построения и анализа является линейное уравнение множественной регрессии:
,
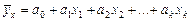где a 0 – свободный член;
a 1, a 2, …, ak – коэффициенты регрессии (параметры модели);
x 1, x 2, …, xk – факторные признаки.
Параметры уравнения можно определить методом наименьших квадратов. Если связь между признаками является нелинейной, то выбранная для ее описания нелинейная многофакторная модель (показательная, степенная и т. д.) сводится к линейной путем линеаризации.
При использовании уравнения регрессии в решении конкретной задачи необходимо учитывать следующие условия построения уравнения регрессии:
· однородность исходных данных;
· небольшое число рассматриваемых переменных;
· отсутствие дублирующих переменных.
Для проверки достоверности уравнения регрессии применяется соотношение
,
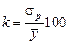где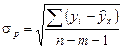 
– стандартная ошибка регрессии;
m – число факторных признаков в уравнении
регрессии.
Считается, что если значение величины k не превысит
10–15 %, то уравнение регрессии достаточно хорошо отображает изучаемую совокупность.
10.5. Показатели тесноты связи
между количественными признаками
Статистическое изучение взаимосвязей социально-экономи-
ческих явлений предполагает измерение тесноты (силы) и направления связи. Нахождение уравнения регрессии сопровождается измерением тесноты связи между признаками. Связь между количественными признаками измеряется через их вариацию. При измерении тесноты корреляционной связи ставится задача – определить, в какой мере вариация результативного признака вызвана вариацией факторного признака.
Теснота связи между количественными признаками измеряется с помощью следующих показателей:
· линейного коэффициента корреляции Пирсона rxy;
· эмпирического h эмп и теоретического корреляционного отношения h теор;
· коэффициента Фехнера K Ф;
· ранговых коэффициентов связи Спирмена (ρ) и Кендалла (τ);
· коэффициента конкордации W.
Линейный коэффициент корреляции rxy применяется для измерения тесноты парной линейной связи. При расчете коэффициента учитывается величина отклонений признаков от средних значений:
.
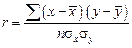После преобразования данной формулы можно получить следующее выражение для расчета линейного коэффициента корреляции:
.
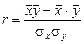В статистике используются различные модификации формулы расчета данного коэффициента:
;
,
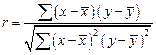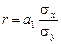где a 1 – коэффициент регрессии в уравнении связи;
s x, s y – среднее квадратическое отклонение соответствующего фак-
торного признака. Знаки коэффициентов регрессии и кор-
реляции совпадают.
Линейный коэффициент корреляции может принимать значе-
ния от –1 до +1: –1 £ r £ +1. Знак «минус» означает, что связь об-
ратная, а знак «плюс» свидетельствует о наличии прямой связи.
Интерпретация значений коэффициента корреляции представлена в табл. 10.2.
Таблица 10.2
Оценка линейного коэффициента корреляции r
| Значение коэффициента r | Характер связи | Интерпретация связи |
| –1 < r < 0 | Обратная | С увеличением x уменьшается y, и наоборот |
| r = 0 | Отсутствует | – |
| 0 < r < 1 | Прямая | С увеличением x увеличивается y |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
Таким образом, линейный коэффициент парной корреляции одновременно характеризует тесноту и направление связи. Коэффициент корреляции является симметричной мерой связи между признаками x и y, т. е. rxy = ryx.
Рассмотрим порядок проверки коэффициента корреляции
на значимость (существенность). Коэффициент корреляции
является выборочным показателем, поэтому он может содержать случайную ошибку, и не всегда однозначно отражать
реальную связь между изучаемыми показателями. Поэтому,
для того чтобы оценить существенность (значимость) самого коэффициента и реальность измеряемой связи, необходимо рассчитать среднюю квадратическую ошибку коэффициента кор-
реляции s r.
Для оценки существенности (значимости) линейного коэффициента корреляции необходимо сопоставить его со средней квадратической ошибкой:
.
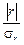Если число наблюдений n £ 30, то средняя ошибка линейного коэффициента корреляции определяется по формуле
.
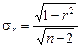Значимость линейного коэффициента корреляции проверяется на основе t -критерия Стьюдента:
.
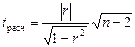При этом выдвигается и проверяется нулевая гипотеза
(H 0: rxy = 0) о равенстве коэффициента корреляции нулю (гипоте-
за об отсутствии связи между х и у в генеральной совокупности).
Если нулевая гипотеза верна, т. е. r = 0, то распределение
t -критерия подчиняется закону Стьюдента с заданными параметрами: уровнем значимости a (обычно принимается за 0,05)
и числом степеней свободы n = n – 2.
По таблице распределения Стьюдента (приложение 5) находится критическое значение t табл, которое допустимо при справедливости нулевой гипотезы. С этим значением сравнивается фактическое (расчетное) значение t расч.
При этом, если t расч > t табл , то нулевая гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции. Следовательно, связь между х и у является статистически существенной (реальной).
Если t расч < t табл , то нулевая гипотеза не отвергается. Коэффициент корреляции считается незначимым (значение r ¹ 0 получено случайно), связь между х и у отсутствует.
Величина r 2 носит название коэффициента детерминации. Он показывает, в какой степени результативный признак зависит от факторного признака. Очевидно, что чем ближе коэффициент к 100 %, тем теснее выявленная зависимость между признаками.
С помощью линейного коэффициента связи r и коэффициента детерминации r 2 можно определить тесноту линейной связи между двумя признаками (табл. 10.3).
Таблица 10.3
