2015-10-13
1515
| Значение коэффициента корреляции | Теснота связи | Значение коэффициента детерминации, % |
| 0,1–0,3 | Слабая | До 10 |
| 0,3–0,5 | Умеренная | 10–25 |
| 0,5–0,7 | Заметная | 25–50 |
| 0,7–0,9 | Тесная | 50–80 |
| 0,9–0,99 | Весьма тесная | 80 и более |
Пример 10.1. Имеются данные по восьми однотипным фирмам
о часовой оплате труда х и уровне текучести кадров у.
| Часовая оплата труда х, руб. | ||||||||
| Уровень текучести кадров у, % |
Требуется:
1) найти уравнение регрессии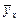 
(уравнение зависимости уровня текучести кадров от величины часовой оплаты труда);
2) измерить тесноту связи между признаками х и у.
Решение. Для решения задачи построим вспомогательную таблицу (табл. 10.4).
1) Применяя метод приведения параллельных данных, видим, что
с ростом значений признака х значения признака у убывают. Поэтому
с помощью графика зависимости у = у (х) можно предположить, что зависимость между х и у обратная, линейная.
Для построения линейного уравнения регрессии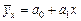 
найдем параметры а 0 и а 1:
Таблица 10.4
Расчетная таблица
для определения линейного коэффициента корреляции
| № п/п | Часовая оплата труда, руб. х | Уровень теку- чести кадров, % у | х 2 | х у | 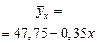 | у 2 |
| 37,25 | ||||||
| 33,75 | ||||||
| 30,25 | ||||||
| 26,75 | ||||||
| 23,25 | ||||||
| 19,75 | ||||||
| 16,25 | ||||||
| 12,75 | ||||||
| Σ | ||||||
| Средняя величина | ||||||
 |  |  |  |  |
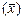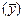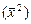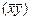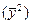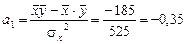– коэффициент регрессии, показывает насколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.
Последовательно подставляя в это уравнение значения х = 30, 40, 50 и т. д., получаем выровненные (теоретические) значения результативного показателя 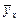(гр. 6 табл. 10.4).
Выровненные уровни 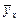показывают, каким теоретически должен быть средний уровень текучести кадров при данной часовой оплате труда хi (при прочих равных условиях для всех предприятий).
2) Для измерения тесноты связи между х и у применим формулу линейного коэффициента корреляции rху, так как связь линейная
и число признаков равно двум.
2.1. Линейный коэффициент корреляции: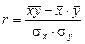 
.
;
; 
;
; 
;
;
.
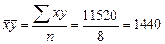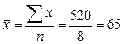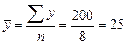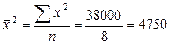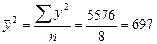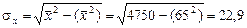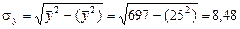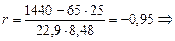связь обратная, весьма тесная,
так как r < 0и 0,9 < r < 0,99.
2.2. Воспользуемся еще одной формулой линейного коэффициента корреляции:
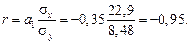
Таким образом, между оплатой труда х и уровнем текучести кад-
ров у существует сильная обратная связь, т. е. с увеличением оплаты труда текучесть кадров снижается.
Теснота связи при нелинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое
и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по формуле
,
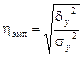где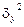 
– межгрупповая дисперсия результативного признака, опре-
деляемая по формуле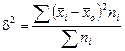 
;
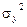– общая дисперсия результативного признака, определяемая
по формуле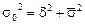 
.
Теоретическое корреляционное отношение рассчитывается по формуле
,
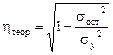где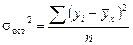 
– остаточная дисперсия, отражающая ва-
риацию результативного признака за счет факторов, не уч-
тенных в уравнении регрессии. Значит, общая дисперсия
эмпирического ряда y равна сумме факторной и остаточной
дисперсий: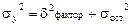 
;
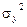– дисперсия эмпирических (фактических) значений результа-
тивного признака.
В данном виде корреляционное отношение при криволинейной зависимости обычно называют индексом корреляции.
Корреляционное отношение h показывает только силу связи и изменяется в пределах от 0 до 1 (0 £ h £ 1). Направление связи определяют по групповым и корреляционным таблицам. Корреляционное отношение применимо для парной и множественной корреляции независимо от формы связи.
С помощью корреляционного отношения можно оценить тесноту связи при линейной и нелинейной зависимости между признаками (табл. 10.4).
Таким образом, в аналитических группировках для характеристики тесноты связи между признаками сопоставляют межгрупповую дисперсию с общей дисперсией. Такое сопоставле-
Таблица 10.4
