Центр инерции
Рассмотрим систему материальных точек (рис. 2.10). Точка с координатами 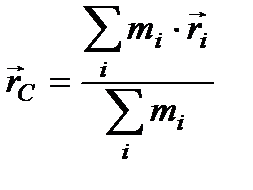 называется центром инерции или центром масс этой системы.
называется центром инерции или центром масс этой системы.
| N |
| i |
| C |
| Рисунок 2.10. К выводу положения центра инерции C системы, состоящей из N материальных точек. |
| y |
| x |
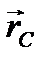 |
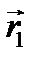 |
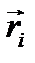 |
Если надо найти центр инерции твёрдого тела (рис. 2.11), то это тело надо разбить на бесконечно малые объемы dV массой dm и заменить суммирование интегрированием:
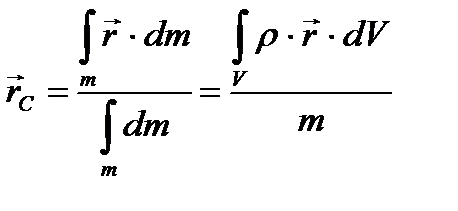
Рисунок 2.11. К выводу формулы центра инерции С абсолютно твёрдого тела массой m и плотностью ρ относительно оси AB. Радиус-вектор бесконечно малого объёма dV массой dm, обозначенного кубиком, равен 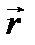 . . |
| y |
| x |
 |
 |
| С |
Момент силы
Вращающее действие силы определяется ее моментом. Моментом 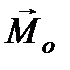 силы
силы 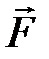 относительно какой-либо точки
относительно какой-либо точки  называется векторное произведение
называется векторное произведение
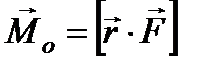
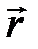 - радиус-вектор, проведенный из точки
- радиус-вектор, проведенный из точки  в точку приложения силы (рис.2.12). Единица измерения момента силы
в точку приложения силы (рис.2.12). Единица измерения момента силы 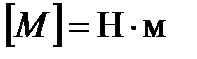 .
.
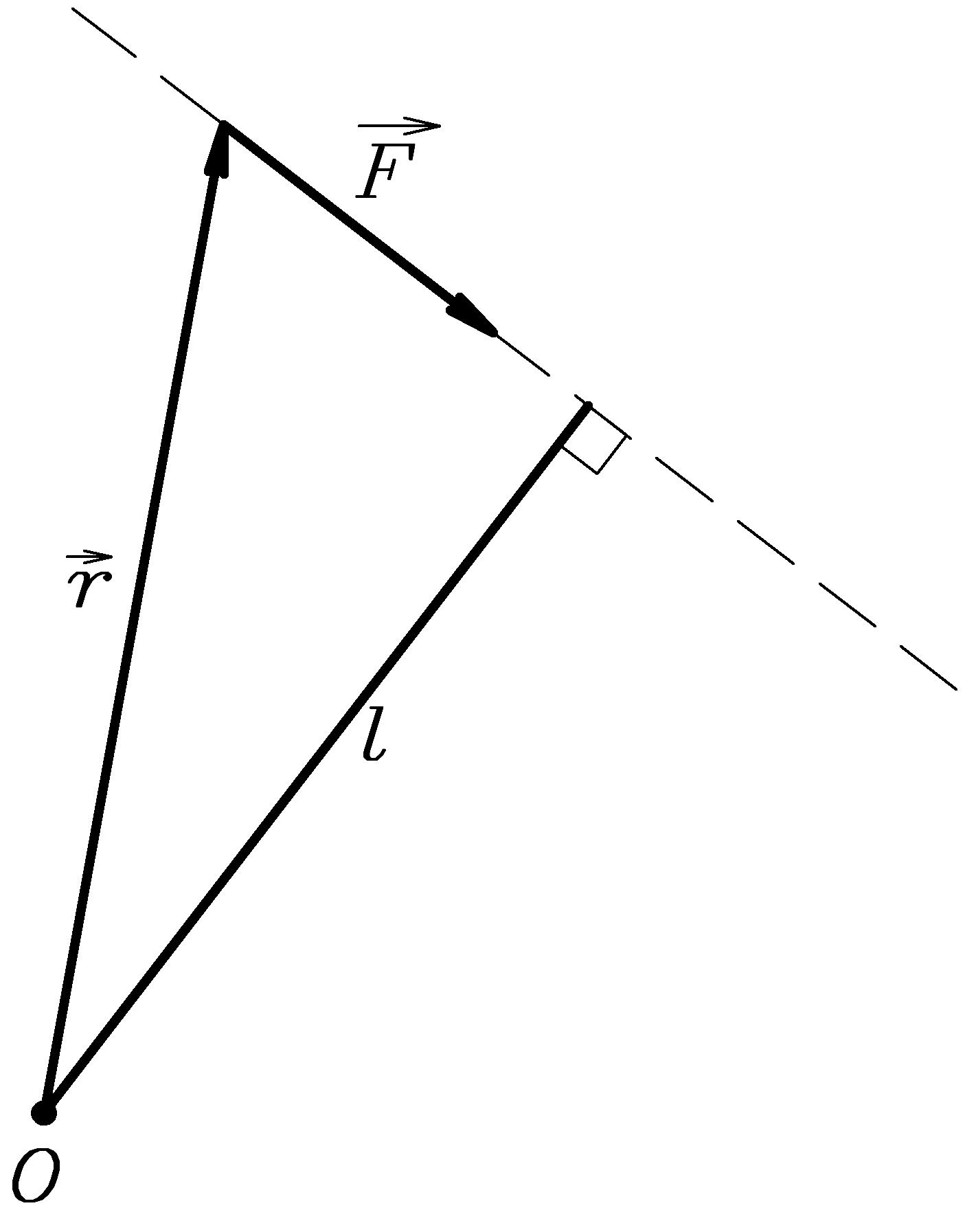
Рисунок 2.12
Величина момента силы
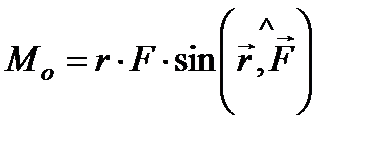 ,
,
или можно записать
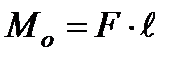
где 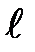 - плечо силы (кратчайшее расстояние от точки
- плечо силы (кратчайшее расстояние от точки  до линии действия силы).
до линии действия силы).
Направление вектора 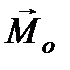 определяется по правилу векторного произведения или по правилу «правого винта» (векторы
определяется по правилу векторного произведения или по правилу «правого винта» (векторы 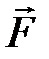 и
и 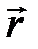 параллельным переносом совмещаем в точке О, направление вектора
параллельным переносом совмещаем в точке О, направление вектора 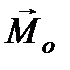 определяется так, чтобы из его конца поворот от вектора
определяется так, чтобы из его конца поворот от вектора 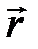 к
к 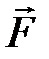 был виден против часовой стрелки – на рис 2.12 вектор
был виден против часовой стрелки – на рис 2.12 вектор 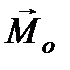 направлен перпендикулярно плоскости чертежа «от нас» (аналогично по правилу буравчика – поступательное движение соответствует направлению вектора
направлен перпендикулярно плоскости чертежа «от нас» (аналогично по правилу буравчика – поступательное движение соответствует направлению вектора 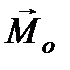 , вращательное соответствует повороту от
, вращательное соответствует повороту от 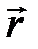 к
к 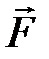 )).
)).
Момент силы относительно какой-либо точки равен нулю, если линия действия силы проходит через эту точку.
Проекция вектора 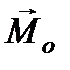 на какую-либо ось, например, ось z, называется моментом
на какую-либо ось, например, ось z, называется моментом 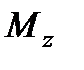 силы
силы 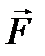 относительно этой оси. Чтобы определить момент силы
относительно этой оси. Чтобы определить момент силы 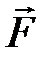 относительно оси, сначала проецируют силу на плоскость, перпендикулярную оси (рис. 2.13), а затем находят момент этой проекции относительно точки пересечения оси с перпендикулярной ей плоскостью. Если линия действия силы параллельна оси, или пересекает ее, то момент силы относительно этой оси равен нулю.
относительно оси, сначала проецируют силу на плоскость, перпендикулярную оси (рис. 2.13), а затем находят момент этой проекции относительно точки пересечения оси с перпендикулярной ей плоскостью. Если линия действия силы параллельна оси, или пересекает ее, то момент силы относительно этой оси равен нулю.
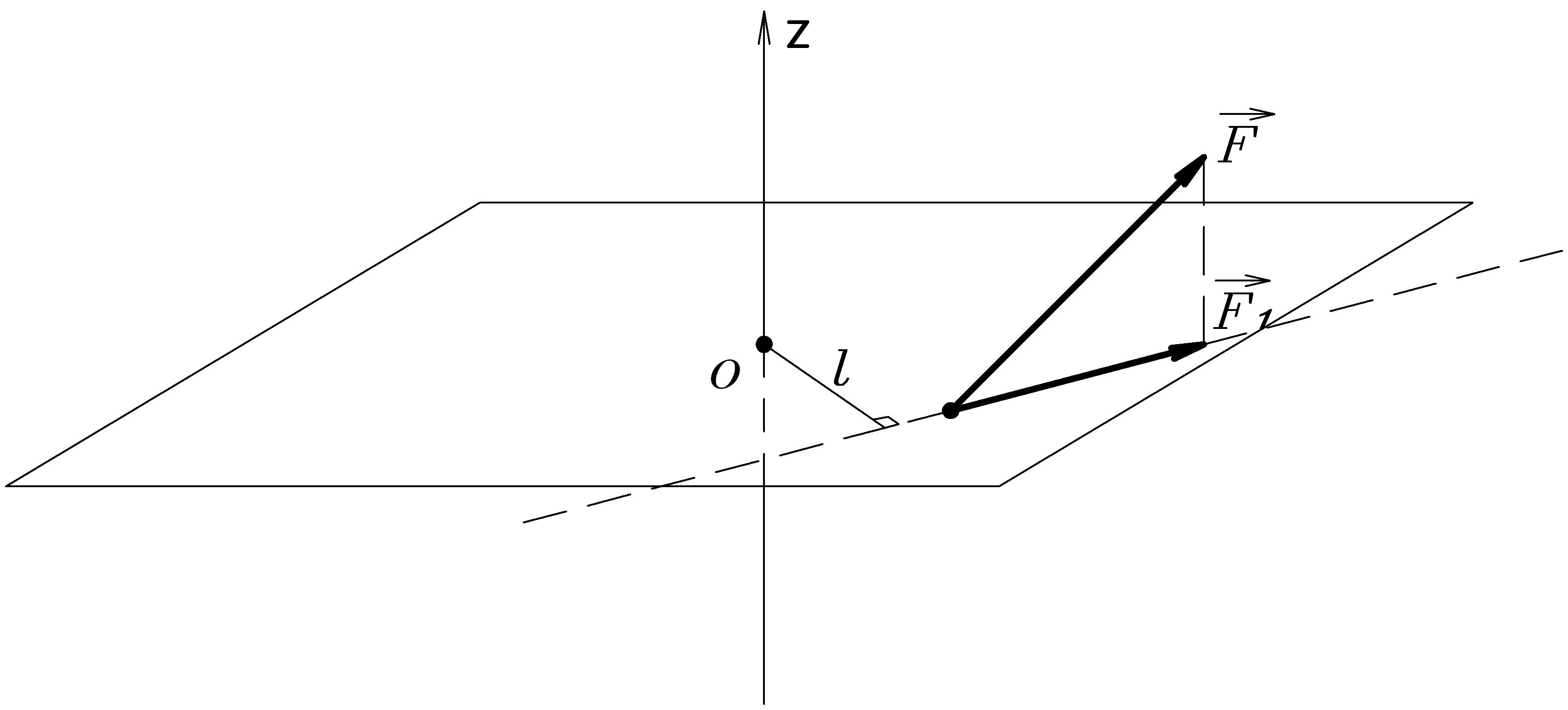
Рисунок 2.13
Момент импульса
Моментомимпульса 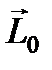 материальной точки массой
материальной точки массой 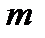 , движущейся со скоростью
, движущейся со скоростью 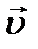 , относительно какой-либо точки отсчета
, относительно какой-либо точки отсчета  , называют векторное произведение
, называют векторное произведение
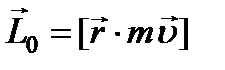 ,
,
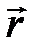 - радиус-вектор материальной точки (рис. 2.14),
- радиус-вектор материальной точки (рис. 2.14), 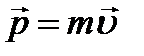 - ее импульс.
- ее импульс.
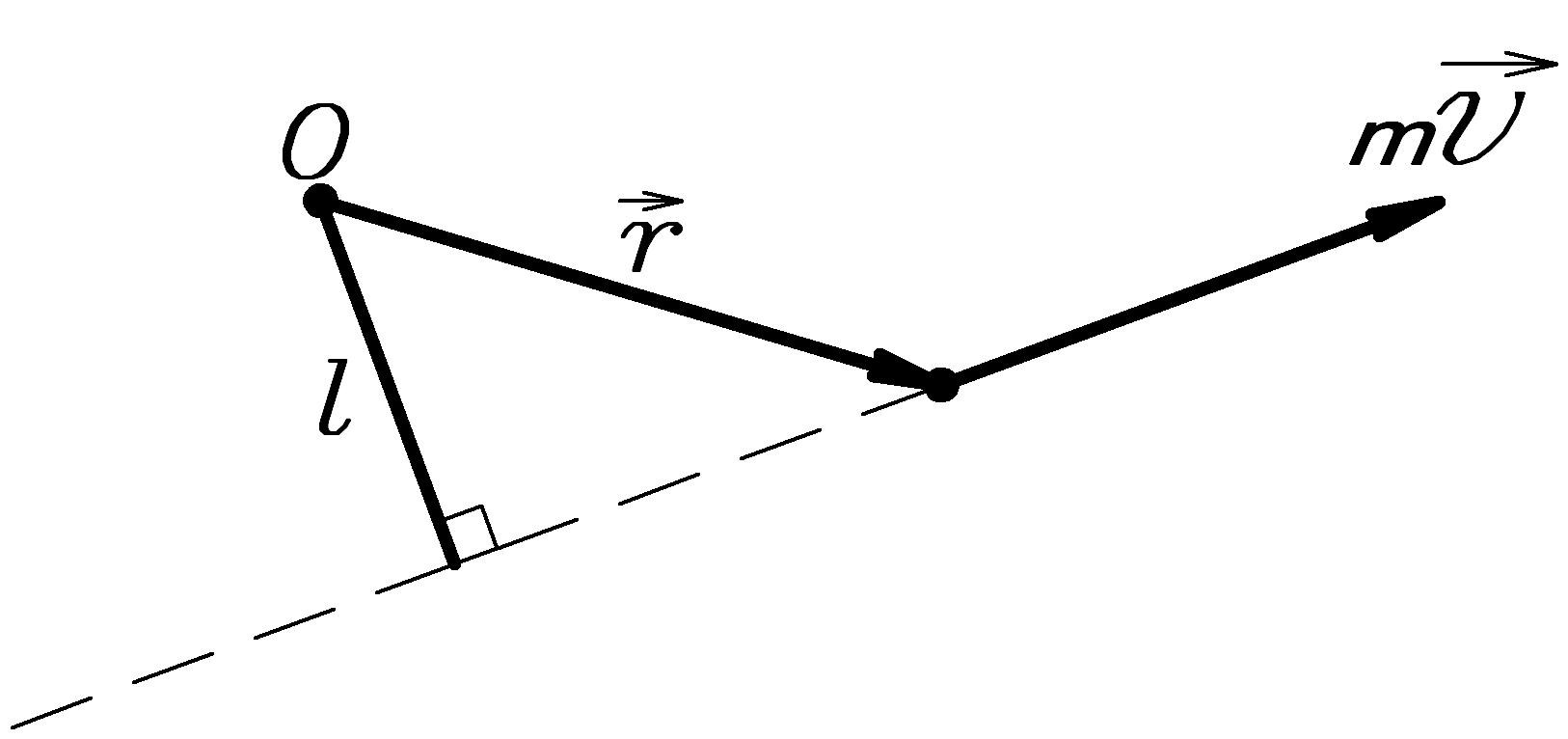
Рисунок 2.14
Величина момента импульса материальной точки
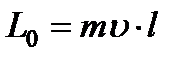 ,
,
где 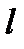 -кратчайшее расстояние от линии вектора
-кратчайшее расстояние от линии вектора 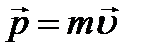 до точки
до точки  .
.
Направление момента импульса определяется аналогично направлению момента силы.
Если выражение для L0 умножить и разделить на l получим:
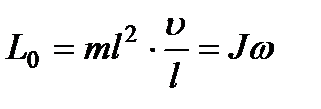
Где 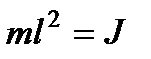 - момент инерции материальной точки - аналог массы во вращательном движении.
- момент инерции материальной точки - аналог массы во вращательном движении.
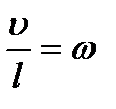 - угловая скорость.
- угловая скорость.
Момент инерции твердого тела
Видно, что получающиеся формулы очень похожи на выражения для импульса и для второго закона Ньютона соответственно, только вместо линейной скорости и ускорения используются угловые скорость и ускорение, а вместо массы – величина I=mR 2, именуемая моментом инерции материальной точки.
Если тело нельзя считать материальной точкой, но можно считать абсолютно твердым, то его момент инерции можно считать суммой моментов инерции бесконечно малых его частей, поскольку угловые скорости вращения этих частей одинаковы (рис. 2.16). Сумма бесконечно малых – интеграл:
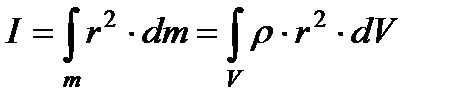
| A |
| B |
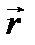 |
Рисунок 2.16. К выводу момента инерции абсолютно твёрдого тела плотностью ρ относительно оси AB. Бесконечно малый объём dV массой dm, обозначенный кубиком, находится на расстоянии 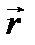 от оси вращения. от оси вращения. |
Для любого тела существуют оси, проходящие через его центр инерции, обладающие таким свойством: при вращении тела вокруг таких осей в отсутствии внешних воздействий оси вращения не меняют своего положения. Такие оси называются свободными осями тела. Можно доказать, что для тела любой формы и с любым распределением плотности существуют три взаимно перпендикулярные свободные оси, именуемые главными осями инерции тела. Моменты инерции тела относительно главных осей именуются главными (собственными) моментами инерции тела.
Главные моменты инерции некоторых тел приведены в табл.:
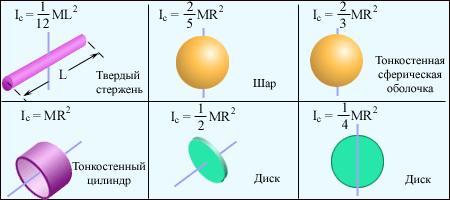
Теорема Гюйгенса-Штейнера.
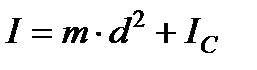 .
.
Это выражение носит название теоремы Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
Основное уравнение динамики вращательного движения
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
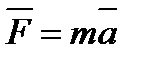
Где F – сила, приложенная к телу массой m; а – линейное ускорение тела.
Если к твердому телу массой m в точке А (рис. 2.15) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение ε и соответственные линейные ускорения, как если бы на каждую точку действовала сила F1…Fn. Для каждой материальной точки можно записать:
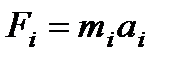
Где 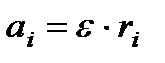 поэтому
поэтому
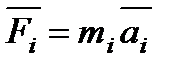
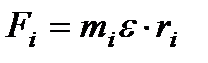
Где mi – масса i- й точки; ε – угловое ускорение; ri – ее расстояние до оси вращения.
Умножая левую и правую части уравнения на ri, получаем
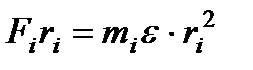
Где 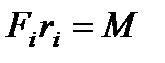 – момент силы – это произведение силы на ее плечо.
– момент силы – это произведение силы на ее плечо.
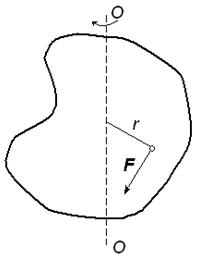
Рис. 2.15. Твердое тело, вращающееся под действием силы F около оси “ОО”
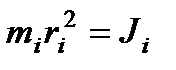 – момент инерции i -й материальной точки (аналог массы во вращательном движении).
– момент инерции i -й материальной точки (аналог массы во вращательном движении).
Выражение можно записать так:
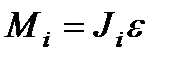
Просуммируем левую и правую части по всем точкам тела:
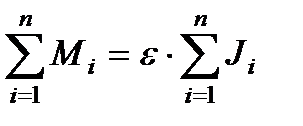 .
.
Или
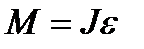
Уравнение – основной закон динамики вращательного движения твердого тела. Величина 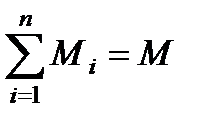 – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение ε.
– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение ε. 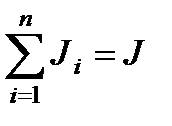 – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
С другой стороны
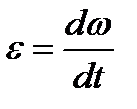
Тогда
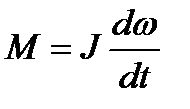
В свою очередь 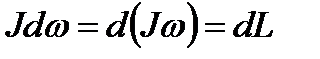 - изменение момента импульса тела.
- изменение момента импульса тела.
Тогда основной закон динамики вращательного движения можно переписать в виде:
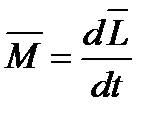
Или 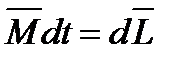 - импульс момента силы
- импульс момента силы 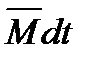 , действующий на вращающееся тело, равен изменению его момента импульса
, действующий на вращающееся тело, равен изменению его момента импульса 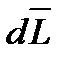 .
.
Закон сохранения момента импульса
Аналогично ЗСИ.
Согласно основному уравнению динамики вращательного движения момент силы относительно оси Z: 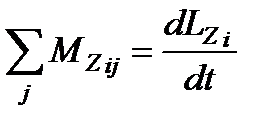 . Отсюда в замкнутой системе
. Отсюда в замкнутой системе 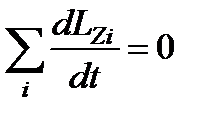 и, следовательно,
и, следовательно, 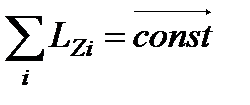 – суммарный момент импульса относительно оси Z всех тел, входящих в замкнутую систему есть величина неизменная. Это выражает закон сохранения момента импульса. Этот закон действует только в инерциальных системах отсчёта.
– суммарный момент импульса относительно оси Z всех тел, входящих в замкнутую систему есть величина неизменная. Это выражает закон сохранения момента импульса. Этот закон действует только в инерциальных системах отсчёта.
Проведем аналогию между характеристиками поступательного движения и вращательного:
| Поступательное движение | Вращательное движение |
| m – масса м.т. | J=mr2 – момент инерции м.т. |
| P = mV – импульс м.т. | L = Jw – момент импульса |
| F - сила | M = [r,F] – момент силы |
F = ma – осн закон динамики пост. движ 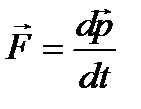 | M=Jw – осн. Зак. Дин. Вр. Движ. 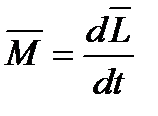 |
 2015-10-13
2015-10-13 6523
6523