1. Момент инерции материальной точки массой m относительно произвольной оси
 ,
,
где r – расстояние от точки до оси.
2. Момент инерции механической системы, состоящей из n материальных точек, относительно произвольной оси равен сумме произведений масс этих точек на квадраты их расстояний  до рассматриваемой оси
до рассматриваемой оси
 ,
,
где mi – масса i -ой материальной точки.
3. Момент инерции тела массой m относительно оси, проходящей через центр масс:
а) полого тонкостенного цилиндра (обруча) относительно оси цилиндра (для обруча относительно оси, перпендикулярной его плоскости)
 ,
,
где R – радиус цилиндра (обруча);
б) сплошного однородного цилиндра (диска) относительно оси цилиндра
 ,
,
где R – радиус цилиндра (диска);
в) однородного шара радиусом R
 ;
;
г) однородного стержня относительно оси, проходящей через его середину перпендикулярно к нему:
 ,
,
где l – длина стержня.
4. Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции  тела относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями
тела относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями
 .
.
5. Моментом силы 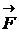 относительно некоторой точки O называют векторную величину
относительно некоторой точки O называют векторную величину  , которая определяется выражением:
, которая определяется выражением:
 ,
,
|
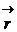 – радиус-вектор, проведенный из точки О в точку приложения силы; [
– радиус-вектор, проведенный из точки О в точку приложения силы; [ 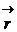
 ] – векторное произведение векторов
] – векторное произведение векторов  и
и 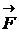 .
.
|
|
|
|
 Вектор
Вектор  перпендикулярен к плоскости, в которой лежат векторы
перпендикулярен к плоскости, в которой лежат векторы  и
и 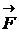 . Направление вектора
. Направление вектора  определяют по правилу правого винта: вектор
определяют по правилу правого винта: вектор  направлен в сторону поступательного движения острия правого винта, головка которого вращается по кратчайшему пути от первого множителя ко второму.
направлен в сторону поступательного движения острия правого винта, головка которого вращается по кратчайшему пути от первого множителя ко второму.
|
|
ветствии с этим правилом вектор

изображен на рис. 4 кружком с вписан- Рис.4
ным в него крестиком.
Числовое значение вектора  равно
равно
 ,
,
где  – угол между направлениями векторов
– угол между направлениями векторов 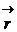 и
и  .
.
6. Моментом силы 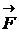 относительно оси z называют параллельную этой оси составляющую момента силы относительно точки О (лежащей на оси)
относительно оси z называют параллельную этой оси составляющую момента силы относительно точки О (лежащей на оси)
 [
[ 
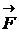 ] z.
] z.
7. Момент импульса материальной точки относительно точки О (рис. 5)

 = [
= [ 
 ] = m [
] = m [ 
 ],
],


 где
где  – радиус-вектор, проведенный из точки О в ту точку пространства, где находится материальная точка массой m;
– радиус-вектор, проведенный из точки О в ту точку пространства, где находится материальная точка массой m;  – импульс точки.
– импульс точки.
 Числовое значение момента импульса
Числовое значение момента импульса
 ,
,
 где
где  – угол между векторами
– угол между векторами 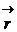 и
и  .
.
8.  Моментом импульса относительно оси z называют составляющую
Моментом импульса относительно оси z называют составляющую  по этой оси момента импульса
по этой оси момента импульса  относительно точки О, лежащей на оси:
относительно точки О, лежащей на оси:
 = [
= [ 
 ] z.
] z.
9. Проекция вектора момента импульса твердого тела (материальной точки) на ось z
 ,
,
где  – проекция вектора угловой скорости на ось z; I z – момент инерции тела относительно оси z.
– проекция вектора угловой скорости на ось z; I z – момент инерции тела относительно оси z.
10. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси
 .
.
Учитывая, что  , уравнение динамики вращательного движения можно записать так:
, уравнение динамики вращательного движения можно записать так:
 ,
,
где  – проекция вектора углового ускорения на ось вращения.
– проекция вектора углового ускорения на ось вращения.
Уравнения для твердого тела справедливы и для системы тел, если считать, что момент импульса системы тел (материальных точек)  , а сумма моментов всех внешних сил
, а сумма моментов всех внешних сил  .
.
11. Закон сохранения момента импульса: момент импульса замкнутой механической системы с течением времени не изменяется
 .
.
Пример 5. Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием силы натяжения невесомой нерастяжимой нити, к концам которой подвешены грузы массами m 1 = 0,3 кг и m 2 = 0,7кг. Определить силы натяжения нити по обе стороны блока.
Дано: m = 0,4кг; m 1 = 0,3 кг; m 2 = 0,7кг; g = 9,81 м/с2.
Найти: Т 1; Т 2.
|
|


|
|


|
|
 и сила натяжения нити
и сила натяжения нити  . Так как m 1 < m 2, то первый груз будет подниматься вверх, а второй – опускаться вниз. Диск будет вращаться по часовой стрелке.
. Так как m 1 < m 2, то первый груз будет подниматься вверх, а второй – опускаться вниз. Диск будет вращаться по часовой стрелке.
|
|
|
|
 ;
;  .
.
|
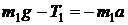 ;
;  .
.
Тогда
 . (1)
. (1)
Со стороны нити на диск действуют силы натяжения  и
и 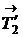 . Вращающий момент, создаваемый этими силами относительно оси z, проходящей через центр диска и направленной перпендикулярно плоскости рисунка от нас:
. Вращающий момент, создаваемый этими силами относительно оси z, проходящей через центр диска и направленной перпендикулярно плоскости рисунка от нас:
 ,
,
где R – радиус диска.
Так как нить по условию задачи невесомая, то  ;
;  . Тогда
. Тогда
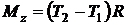 .
.
Запишем уравнение динамики вращательного движения для диска
 .
.
Так как  ,
,  , то, делая подстановку, можем записать
, то, делая подстановку, можем записать
 ;
;  .
.
Подставив выражения (1), определяющие Т 1 и Т 2, после несложных преобразований получим
 .
.
Подставим числовые значения
 м/с2.
м/с2.
Найдем значения Т 1 и Т 2:
 Н;
Н;
 Н.
Н.
Ответ: Т 1 = 3,9 Н; Т 2 = 4,6 Н.
Пример 6. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вдоль оси вращения скамейки (вертикально). Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой  . Радиус R колеса равен 20 см, его масса m = 3 кг. Определить частоту вращения скамьи n, если человек повернет стержень на угол 180°. Суммарный момент инерции человека и скамьи I = 6 кг×м2. Масса колеса равномерно распределена по ободу.
. Радиус R колеса равен 20 см, его масса m = 3 кг. Определить частоту вращения скамьи n, если человек повернет стержень на угол 180°. Суммарный момент инерции человека и скамьи I = 6 кг×м2. Масса колеса равномерно распределена по ободу.
Дано:  ; R = 0,2 м; m = 3 кг;
; R = 0,2 м; m = 3 кг;  кг×м2; α= 1800.
кг×м2; α= 1800.
Найти: n.
Решение. Согласно условию задачи момент внешних сил относительно оси вращения z можно считать равным нулю. В этом случае проекция вектора момента импульса всей системы (рис.7) на ось z изменяться не будет (закон сохранения момента импульса).
|
|
|
|
|

а) б)
Рис.7
Запишем закон сохранения момента импульса в проекциях на ось z, учитывая, что в начальный момент времени скамья и человек были неподвижны:
 или
или  , (1)
, (1)
где  проекция вектора момента импульса колеса на ось z в начальный момент времени;
проекция вектора момента импульса колеса на ось z в начальный момент времени;  – момент инерции колеса относительно оси z;
– момент инерции колеса относительно оси z;  – угловая скорость колеса;
– угловая скорость колеса;  – проекция вектора момента импульса скамьи и человека на ось z после того, как человек повернул стержень;
– проекция вектора момента импульса скамьи и человека на ось z после того, как человек повернул стержень;  – угловая скорость скамьи;
– угловая скорость скамьи;  – проекция вектора момента импульса колеса на ось z после того, как человек повернул стержень.
– проекция вектора момента импульса колеса на ось z после того, как человек повернул стержень.
Из уравнения (1) выразим ω:
 . (2)
. (2)
Момент инерции колеса, с массой равномерно распределенной по ободу,  . Так как
. Так как  ,
,  , то, делая подстановку в уравнение (2) и произведя сокращения, получим
, то, делая подстановку в уравнение (2) и произведя сокращения, получим
 .
.
Подставим числовые значения и выполним вычисления
 .
.
Ответ:  .
.
ТЯГОТЕНИЕ
 ,
,
где F – сила взаимного притяжения двух материальных точек массами  и
и  ; r – расстояние между точками; G – гравитационная постоянная.
; r – расстояние между точками; G – гравитационная постоянная.
Это уравнение справедливо также для взаимодействующих тел, представляющих собой однородные шары. В этом случае r – расстояние между центрами масс шаров.
2. Напряженность гравитационного поля
 ,
,
где  – сила, действующая на материальную точку массой
– сила, действующая на материальную точку массой  в данной точке гравитационного поля.
в данной точке гравитационного поля.
Напряженность гравитационного поля вблизи поверхности Земли приближенно равна ускорению свободного падения.
3. Сила тяжести
 ,
,
где  – ускорение свободного падения.
– ускорение свободного падения.
4. Весом тела  называют силу, с которой тело вследствие тяготения действует на опору или подвес.
называют силу, с которой тело вследствие тяготения действует на опору или подвес.
5. Потенциальная энергия гравитационного взаимодействия двух материальных точек массами  и
и  , находящихся на расстоянии r друг от друга:
, находящихся на расстоянии r друг от друга:
 .
.
6. Потенциал гравитационного поля
 ,
,
где  – потенциальная энергия материальной точки массой
– потенциальная энергия материальной точки массой  , помещенной в данную точку поля.
, помещенной в данную точку поля.
7. Первой космической скоростью называют такую минимальную скорость, которую следует сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, то есть превратиться в искусственный спутник Земли.
8. Второй космический скоростью называют такую наименьшую скорость, которую следует сообщить телу, чтобы оно могло без воздействия каких-либо дополнительных сил преодолеть земное притяжение и превратиться в искусственный спутник Солнца.
РАБОТА И ЭНЕРГИЯ
1. Работа силы  на пути
на пути 
 ,
,
где α – угол между направлением силы и направлением движения точки приложения силы.
В случае постоянной силы  , действующей под углом α к перемещению:
, действующей под углом α к перемещению:
 .
.
2. Мгновенная мощность
 ,
,
где 
 – скалярное произведение векторов
– скалярное произведение векторов  и
и  ; α – угол между векторами
; α – угол между векторами  и
и  .
.
3. Кинетическая энергия тела массой m, движущегося поступательно со скоростью υ:
 .
.
4. Потенциальная энергия тела массой  , поднятого на высоту
, поднятого на высоту  над поверхностью Земли:
над поверхностью Земли:
 ,
,
где h – высота, отсчитываемая от нулевого уровня, для которого  .
.
Эта формула справедлива при условии  , где
, где  – радиус Земли.
– радиус Земли.
5. Сила упругости
 ,
,
где  – коэффициент упругости (в случае пружины – жёсткость);
– коэффициент упругости (в случае пружины – жёсткость);  – величина деформации.
– величина деформации.
6. Потенциальная энергия упругодеформированного тела (пружины)
 .
.
7. Кинетическая энергия тела массой  , вращающегося относительно оси z:
, вращающегося относительно оси z:
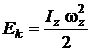 ,
,
где  – момент инерции тела относительно оси вращения;
– момент инерции тела относительно оси вращения;  – проекция вектора угловой скорости на ось z.
– проекция вектора угловой скорости на ось z.
8. Кинетическая энергия тела, участвующего в поступательном и вращательном движениях:
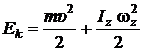 ,
,
где υ – скорость центра масс тела;  – момент инерции тела относительно оси вращения, проходящей через центр масс.
– момент инерции тела относительно оси вращения, проходящей через центр масс.
9. Работа внешних сил при вращении твердого тела
 ,
,
где  – проекция результирующего момента приложенных к телу внешних сил на ось z;
– проекция результирующего момента приложенных к телу внешних сил на ось z;  – угол, на который поворачивается тело за время
– угол, на который поворачивается тело за время  .
.
10. Закон сохранения механической энергии: в замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия с течением времени не изменяется
 .
.
Пример 7. Из бесконечности на поверхность Земли падает метеорит массой  = 30 кг. Определить работу
= 30 кг. Определить работу  , которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения
, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения  у поверхности Земли и её радиус
у поверхности Земли и её радиус  считать известными.
считать известными.
Дано:  = 30 кг;
= 30 кг;  = 9,81 м/с2;
= 9,81 м/с2;  = 6,37×106 м.
= 6,37×106 м.
Найти:  .
.
Решение. Механическую систему Земля-метеорит можно считать замкнутой. Со стороны Земли на метеорит действует сила тяготения. Это сила консервативная, поэтому при движении метеорита в поле тяготения Земли его механическая энергия изменяться не будет.
Так как метеорит был бесконечно далеко удален от Земли, то его потенциальная энергия в начальный момент времени была равна нулю
 ,
,
где 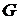 – гравитационная постоянная;
– гравитационная постоянная;  – масса метеорита;
– масса метеорита;  – масса Земли;
– масса Земли;  – расстояние от центра масс Земли до метеорита.
– расстояние от центра масс Земли до метеорита.
Если  , то
, то  . Потенциальная энергия метеорита вблизи поверхности Земли
. Потенциальная энергия метеорита вблизи поверхности Земли
 ,
,
где  – радиус Земли.
– радиус Земли.
В соответствии с законом сохранения механической энергии
 ,
,
где  – кинетические энергии метеорита в начальный момент времени и вблизи поверхности Земли.
– кинетические энергии метеорита в начальный момент времени и вблизи поверхности Земли.
По мере приближения к Земле потенциальная энергия метеорита будет убывать, а его кинетическая энергия – увеличиваться. При движении метеорита в гравитационном поле Земли сила тяготения совершает работу. Эта работа идет на увеличение кинетической энергии метеорита и совершается за счет убыли его потенциальной энергии
 . (1)
. (1)
На метеорит вблизи поверхности Земли действует сила тяготения
 .
.
Если пренебречь суточным вращением Земли, то в соответствии со вторым законом Ньютона  , тогда
, тогда  . Делая подстановку в уравнение (1), получим
. Делая подстановку в уравнение (1), получим  .
.
Выполним вычисления
 .
.
Ответ:  .
.
Пример 8. Диск скатывается без скольжения с наклонной плоскости. Найти линейную скорость υ центра масс диска у основания наклонной плоскости, если ее высота h равна 0,5 м, начальная скорость движения диска υ 0 равна нулю, угол α, который плоскость составляет с горизонтом, равен 30°. Сколько времени будет скатываться диск?
Дано h = 0,5 м; υ 0 = 0 м/с; α = 300;  м/с2.
м/с2.
Найти: υ; t.
Решение. В начальный момент времени кинетическая энергия диска  равна нулю, а его потенциальная энергия
равна нулю, а его потенциальная энергия
 ,
,
где  – масса диска;
– масса диска;  – ускорение свободного падения.
– ускорение свободного падения.
|
|
|
|
|

Рис.8
У основания наклонной плоскости потенциальная энергия диска  равна нулю, а его кинетическая энергия
равна нулю, а его кинетическая энергия
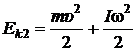 ,
,
где  – кинетическая энергия поступательного движения;
– кинетическая энергия поступательного движения;  – кинетическая энергия вращательного движения;
– кинетическая энергия вращательного движения;  – момент инерции диска относительно его геометрической оси (ось, проходящая через центр масс диска перпендикулярно плоскости рисунка);
– момент инерции диска относительно его геометрической оси (ось, проходящая через центр масс диска перпендикулярно плоскости рисунка);  – угловая скорость диска относительно его геометрической оси.
– угловая скорость диска относительно его геометрической оси.
Так как  ;
;  , где
, где  – радиус диска, то
– радиус диска, то 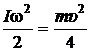 . Тогда
. Тогда
 .
.
В соответствии с законом сохранения механической энергии
 .
.
Делая подстановку, запишем  .
.
Найдем скорость диска у основания наклонной плоскости
 .
.
Подставив числовые значения, получим

 м/с.
м/с.
На диск во время движения действуют постоянные по величине силы. Следовательно, диск будет двигаться с постоянным по модулю ускорением а. В этом случае
 ; (1)
; (1)
 , (2)
, (2)
где  – длина наклонной плоскости.
– длина наклонной плоскости.
Решая уравнения (1) и (2) совместно, найдем время скатывания
 .
.
Выполним вычисления

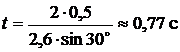 .
.
Ответ: υ  м/с;
м/с;  с.
с.
Пример 9. Пружина жесткостью  сжата силой
сжата силой  . Определить работу
. Определить работу  внешней силы, дополнительно сжимающей пружину еще на
внешней силы, дополнительно сжимающей пружину еще на  .
.
Дано:  ;
;  ;
; 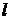 = 2 см = 0,02 м.
= 2 см = 0,02 м.
Найти:  .
.
Решение. Пусть внешняя сила  сжимает пружину на величину
сжимает пружину на величину 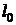 . В соответствии с законом Гука
. В соответствии с законом Гука  . Так как
. Так как  , то потенциальная энергия пружины в этом состоянии
, то потенциальная энергия пружины в этом состоянии
 .
.
Потенциальная энергия пружины, сжатой на величину ( ):
):
 .
.
Работа, совершаемая внешней силой при сжатии пружины, идет на увеличение ее потенциальной энергии. В соответствии с законом сохранения механической энергии
 .
.
Подставим числовые значения
 .
.
Ответ:  .
.
Пример 10. Якорь двигателя вращается с частотой  . Определить вращающий момент
. Определить вращающий момент  , если двигатель развивает мощность
, если двигатель развивает мощность  .
.
Дано:  ;
;  .
.
Найти:  .
.
Решение. При повороте якоря на угол  вращающий момент
вращающий момент  совершает работу
совершает работу
 ,
,
где  – проекция вектора момента силы на ось вращения z.
– проекция вектора момента силы на ось вращения z.
Мощность двигателя
 ,
,
где  – угловая скорость якоря.
– угловая скорость якоря.
Найдем вращающий момент:  . Выполним проверку размерности
. Выполним проверку размерности
 .
.
Выполним вычисления
 .
.
Ответ:  .
.
Пример 11. Кинетическая энергия тела, вращающегося относительно неподвижной оси, зависит от угла поворота  по закону
по закону  . При этом вращающий момент
. При этом вращающий момент  . Найти значение n.
. Найти значение n.
Дано:  ;
;  .
.
Найти: n.
Решение. Пусть тело вращается относительно неподвижной оси z. Его кинетическая энергия равна
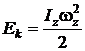 ,
,
где  – момент инерции тела относительно оси вращения;
– момент инерции тела относительно оси вращения;  – проекция вектора угловой скорости на ось z.
– проекция вектора угловой скорости на ось z.
Так как  , то
, то  . Тогда
. Тогда  .
.
Запишем уравнение динамики вращательного движения тела относительно оси z
 или
или  , (1)
, (1)
где  – проекция вектора момента силы на ось
– проекция вектора момента силы на ось  ;
;  – проекция вектора углового ускорения на ось z.
– проекция вектора углового ускорения на ось z.
Делая подстановку  в уравнение (1), получим
в уравнение (1), получим
 ,
,
где  .
.
Ответ:  .
.
 2017-11-30
2017-11-30 1088
1088















