Как было сказано ранее, импульсом материальной точки называется произведение её массы на скорость: 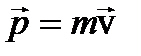 . Для системы из N материальных точек импульс системы равен сумме импульсов материальных точек, входящих в эту систему
. Для системы из N материальных точек импульс системы равен сумме импульсов материальных точек, входящих в эту систему 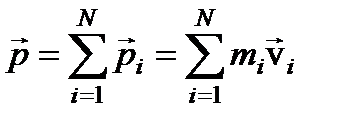 . Тело, которое нельзя считать материальной точкой, можно разделить на бесконечно малые объёмы и, перейдя от суммированию к интегрированию, получить:
. Тело, которое нельзя считать материальной точкой, можно разделить на бесконечно малые объёмы и, перейдя от суммированию к интегрированию, получить: 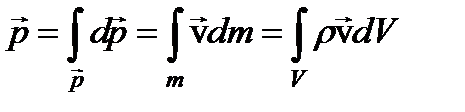 .
.
Или, 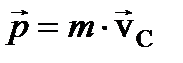 – импульс тела есть произведение массы тела на скорость движения центра масс. Таким образом, тело ведет себя как материальная точка, обладающая всей массой этого тела и находящаяся в центре масс.
– импульс тела есть произведение массы тела на скорость движения центра масс. Таким образом, тело ведет себя как материальная точка, обладающая всей массой этого тела и находящаяся в центре масс.
Введем понятие замкнутой системы.
Система называется замкнутой если на нее не действуют внешние силы.
Рассмотрим замкнутую систему тел – материальных точек (рис. 2.2). Поскольку для каждой силы 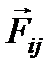 (i – номер тела, на которое действует сила, j – номер тела, со стороны которого действует сила) существует
(i – номер тела, на которое действует сила, j – номер тела, со стороны которого действует сила) существует 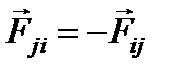 , то
, то 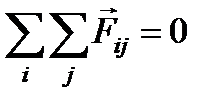 . Таким образом, сумма всех сил, действующих в замкнутой системе тел, равна нулю.
. Таким образом, сумма всех сил, действующих в замкнутой системе тел, равна нулю.
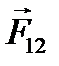 |
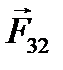 |
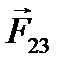 |
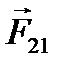 |
| Рисунок 2.2. Силы, действующие в замкнутой системе тел. |
По второму закону Ньютона 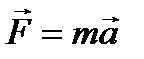 .
.
Ускорение можно представить в виде:
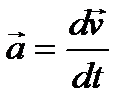
Где v – вектор скорости материальной точки; t – время.
Тогда
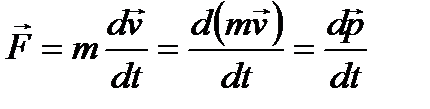
Где p – вектор импульса.
Т.е сумма всех сил, действующих в системе равна:
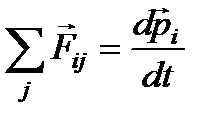 .
.
Отсюда 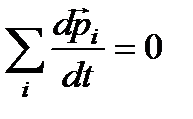 и, следовательно,
и, следовательно, 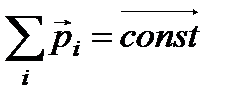 – суммарный импульс всех тел, входящих в замкнутую систему есть величина неизменная. Это выражает закон сохранения импульса. Этот закон действует только в инерциальных системах отсчёта.
– суммарный импульс всех тел, входящих в замкнутую систему есть величина неизменная. Это выражает закон сохранения импульса. Этот закон действует только в инерциальных системах отсчёта.
Если система тел незамкнутая, то, кроме внутренних сил 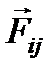 , действуют ещё и внешние силы
, действуют ещё и внешние силы 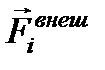 со стороны тел, не входящих в систему (рис. 2.3). В этом случае полная сумма всех сил
со стороны тел, не входящих в систему (рис. 2.3). В этом случае полная сумма всех сил 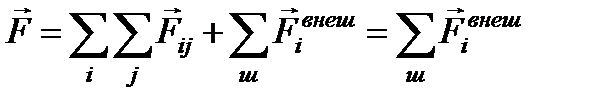 .
.
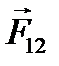 |
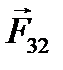 |
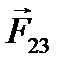 |
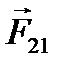 |
| Рисунок 2.3. Силы, действующие в незамкнутой системе тел. |
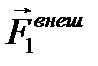 |
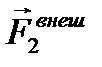 |
x’ 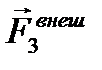 |
В некоторых случаях ЗСИ выполняется для незамкнутых систем:
1. Сумма всех внешних сил равна нулю: 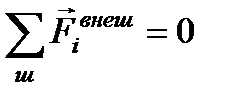 ;
;
2. Время действия внешней силы ничтожно мало (удар);
Если можно выбрать направление (ось), на которое проекция всех внешних сил равна нулю, то и импульс в данном направлении будет сохраняться: 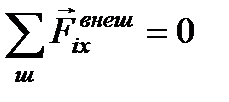 , то
, то 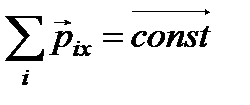
 2015-10-13
2015-10-13 1387
1387
