(учет риска в знаменателе формулы NPV посредством корректировки ставки дисконта)
Первоначальные инвестиции компании в реализацию проекта составили 3 000 у.е. Безрисковая дисконтная ставка составляет 10%. Плата за риск – 5%. Динамика чистых денежных потоков представлена в табл. 3.5.1. Рассчитайте эффективность проекта с учетом и без учета риска.
Таблица 3.5.1 — Динамика чистых денежных потоков
| Год | |||||
| Стоимость денежного потока, у.е. | 1 100 | 2 200 | 2 000 | - 400 | - 1 000 |
Решение:
Для удобства расчетов составим таблицу в Excel (табл. 3.5.2). Рассмотрим в таблице динамику денежных потоков по годам.
Для расчета дисконтированной стоимости денежных потоков воспользуемся формулой:
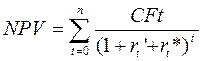
где, CFt — чистый поток средств в год t,
rt’ — безрисковая годовая ставка дисконта в год t,
rt* — премия за риск в год t,
n — количество лет реализации проекта.
Таблица 3.5.2 — Расчет NPV проекта с учетом и без учета риска.
| Годы | ||||||
| I0, тыс. у.е. | ||||||
| r t', % | ||||||
| r t*,% | ||||||
| r t' + r t*, % | ||||||
| CF t, тыс. у.е. | -400 | -1000 | ||||
| Приведенная стоимость чистых денежных потоков (без учета риска) PV t ', тыс. у.е. | 1000,0 | 1818,2 | 1502,6 | -273,2 | -620,9 | |
| Приведенная стоимость чистых денежных потоков (с учетом риска) PVt *, тыс. у.е. | 956,5 | 1663,5 | 1315,0 | -228,7 | -497,2 | |
| Чистая приведенная стоимость (NPV') без учета риска, тыс. у.е. | 426,7 | |||||
| Чистая приведенная стоимость (NPV*) с учетом риска, тыс. у.е. | 209,2 |
Очевидно, что введение премии за риск существенно уменьшает чистую приведенную стоимость проекта, что является обоснованным: инвестор ждет более высокой прибыли от сделок, связанных с риском, чем от безрисковых вложений (например, таких как депозитный вклад в надежном банке). Введение платы за риск также дает возможность сравнивать проекты с разным уровнем риска.
MS Excel позволяет быстро рассчитывать чистую приведенную стоимость с помощью функции ЧПС. Проверьте свои вычисления с ее помощью. Однако данная функция не подходит для тех случаев, когда ставка дисконтирования в разные годы не одинакова (а также, когда нам необходимо учесть поправку на риск, которая тоже может быть разной для нескольких лет).
 2015-10-13
2015-10-13 407
407








