Для этого метода исходная булева функция должна быть представлена в СДНФ. Если эта функция представлена в произвольной ДНФ, то ее с помощью операции развертывания, заключающейся в умножении некоторых членов на выражение вида 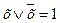 , приводят к СДНФ.
, приводят к СДНФ.
Метод Квайна основан на последовательном применении к парам дизъюнктивных членов операций склеивания и элементарного поглощения.
Операция склеивания основана на справедливости тождества 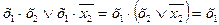 . Операция элементарного поглощения — на справедливости тождеств х 1Ú х 1 х 2 = х 1 и х 1(х 1Ú х 2) = х 1.
. Операция элементарного поглощения — на справедливости тождеств х 1Ú х 1 х 2 = х 1 и х 1(х 1Ú х 2) = х 1.
Вначале в СДНФ исходной булевой функции проводят все возможные операции склеивания дизъюнктивных членов — конъюнкций ранга n, где n — число аргументов функции. В результате склеивания получим конъюнкции n – 1 ранга. После выполнения операции поглощения с конъюнкциями n – 1 ранга осуществляют все возможные операции склеивания конъюнкций n – 1 ранга. Затем проводят операции поглощения с конъюнкциями n – 2 ранга и вновь выполняют операции склеивания и т.д.
|
|
|
Пример 4. Найти сокращенную ДНФ булевой функции
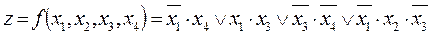
1) Используя операцию развертывания, представим исходную функцию в СДНФ. Для этого первуй член 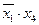 умножим на
умножим на 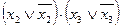 , второй член
, второй член 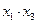 умножим на
умножим на 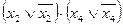 , третий член
, третий член 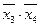 умножим на
умножим на 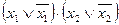 , а четвертый член
, а четвертый член 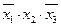 умножим на
умножим на 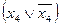 . В результате получим СДНФ:
. В результате получим СДНФ:
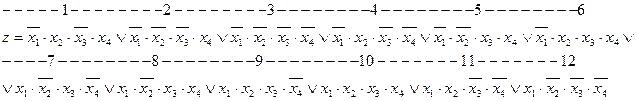
2) Пронумеруем все дизъюнктивные члены.
3) Выполним все возможные операции склеивания дизъюнктивных членов в такой последовательности:
первый член со всеми остальными,
второй член с остальными, кроме первого,
третий член с остальными, кроме первого и второго, и т.д.
В результате проведенных операций склеивания и поглощения получим ДНФ заданной функции в форме
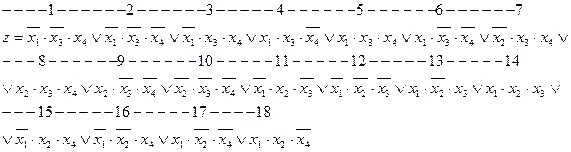
Пронумеровав все члены выражения, полученного на предыдущем этапе, выполним все возможные операции склеивания конъюнкций третьего ранга в той же последовательности, что и ранее. В результате проведенных операций склеивания и поглощения исходная функция примет вид
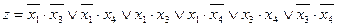 .
.
 2015-10-13
2015-10-13 2646
2646








