Лабораторная работа № 323

ИЗМЕРЕНИЕ СДВИГА ФАЗ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА

Приборы и принадлежности: лабораторная панель «Переменный ток. Закон Ома» с резистором, конденсатором и катушкой, источник переменного тока – генератор Г3-118, универсальный вольтметр В7-40.

Введение. Рассмотрим электрическую цепь (рис.1), содержащую (в общем случае) активное сопротивление R, индуктивность L и емкость C, в которую включен источник переменного тока с напряжением на выходе

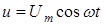, (1)

где u – мгновенное напряжение – напряжение в момент времени t,

U_m – амплитуда напряжения,

w – циклическая частота колебаний напряжения.

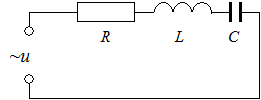Принято считать, что активное сопротивление всей цепи (в том числе сопротивление проводов, сопротивление обмотки катушки) сосредоточено в R, емкость всей цепи – в С, а индуктивность –

в L. Такая цепь называется контуром с сосредоточенными параметрами. Согласно второму правилу Кирхгофа для данной цепи можно написать Рис.1

следующее уравнение:

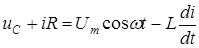, (2)

где i – мгновенное значение тока в цепи, изменяющееся как и напряжение с частотой w,

u_C – напряжение на конденсаторе.

Рассмотрим ряд цепей с различными нагрузками и соответствующие им уравнения.

1. Пусть к источнику присоединено только активное сопротивление R (рис.2, а). При этом L=0, C®µ. Сопротивление называется активным потому, что в нем происходит превращение энергии электрического тока во внутреннюю энергию проводника или в механическую работу.

Уравнение (2) для данного частного случая принимает вид:

,

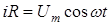из которого следует, что ток

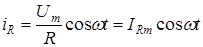, (3)

где I_Rm – амплитуда тока в цепи с активной нагрузкой, I_Rm=U_m/R.

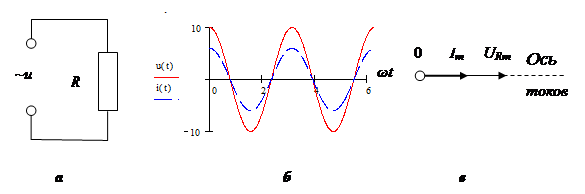Таким образом, колебания силы тока в цепи, содержащей только активное

Рис.2

сопротивление, совпадают по фазе с колебаниями напряжения (рис. 2, б). Векторная диаграмма для данной ситуации представлена на рис. 2, в.

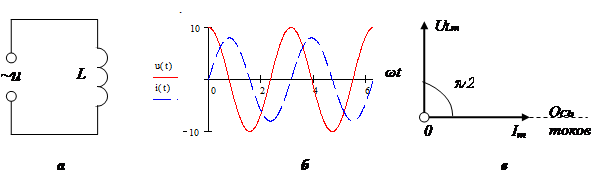2. Пусть нагрузкой источника переменного тока является катушка индуктивности L. Активным и емкостным сопротивлением данной цепи пренебрежом (рис.3, а).

Рис.3

Уравнение Кирхгофа (2) для такого контура имеет вид:

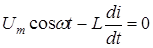. (4)

Величина ЭДС самоиндукции 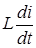численно равна падению напряжения на индуктивности L, которое в дальнейшем обозначим U_L.