Установлению природы пространственного заряда, потенциального характера поля пространства помогает само понятие потенциальности, взаимосвязи материальных объектов.
IV.1. В теории жидкостей и газов (например, [255, с.222¸227]) для описания изменения взаимодействия между молекулами в зависимости от расстояния 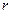 между ними широко применяется потенциал взаимодействия Леннарда-Джонса:
между ними широко применяется потенциал взаимодействия Леннарда-Джонса: 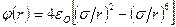 ; при
; при 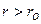 между молекулами действуют силы притяжения; при
между молекулами действуют силы притяжения; при 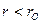 - отталкивания; при
- отталкивания; при 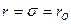 молекулы обладают "нулевой" потенциальной энергией взаимодействия, соответствующей их наиболее плотной упаковке.
молекулы обладают "нулевой" потенциальной энергией взаимодействия, соответствующей их наиболее плотной упаковке.
Почему без затраты дополнительной энергии молекулы (атомы) газа нельзя придвинуть еще ближе друг к другу, что мешает?
Поставим вопрос несколько иначе:
почему атомы и молекулы газов земной атмосферы удерживаются на определенном расстоянии между собой, что мешает их большему сближению, с чем взаимодействует поле сил их ядер?
IV.2. Если исходить из потенциальности энергии пространства разреженной газовой среды (вакуума), то ей должно соответствовать поле сил, обеспечивающих эту потенциальность: по определению механики потенциальной является энергия, обусловленная взаимным положением тел в конкретной области пространства. Поскольку с уменьшением давления газа количество его атомов (молекул) уменьшается, то можно утверждать, что уменьшается и потенциальная энергия газовой среды, обусловленная полем сил ядер ее атомов. Однако здесь вновь возникают вопросы: посредством чего атомы (и молекулы) газа удерживаются на определенном расстоянии между собой, что их удерживает, на что действует их поле сил, что представляет потенциальную энергию газового пространства?
|
|
|
IV.3. Попробуем ответить на следующий вопрос: предполагает ли термодинамический подход к воздушной атмосфере возможность пребывания в ней свободной энергии в качестве свободного пространственного заряда?
Если рассматривать выделенный объем 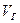 нормального состояния воздушной атмосферы (при
нормального состояния воздушной атмосферы (при 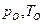 ), то термодинамически устойчивое и связанное состояние всей системы атомов и молекул этого объема должно характеризоваться минимумом свободной энергии
), то термодинамически устойчивое и связанное состояние всей системы атомов и молекул этого объема должно характеризоваться минимумом свободной энергии 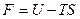 (
(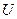 - внутренняя энергия,
- внутренняя энергия, 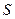 - энтропия системы). Это же состояние характеризуется и максимумом энтропии для всех частиц системы – в равновесном состоянии энтропия
- энтропия системы). Это же состояние характеризуется и максимумом энтропии для всех частиц системы – в равновесном состоянии энтропия 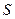 максимальна и характеризует макросостояние системы, осуществляемое посредством максимального числа микросостояний.Уменьшение давления газа в объеме
максимальна и характеризует макросостояние системы, осуществляемое посредством максимального числа микросостояний.Уменьшение давления газа в объеме 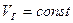 при
при 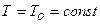 будет происходить при сохранении атомами и молекулами газа своих собственных объемов (учитываемых, например, поправками в уравнении состояния Ван-дер-Ваальса). Область же пространства, приходящая на один атом газа,
будет происходить при сохранении атомами и молекулами газа своих собственных объемов (учитываемых, например, поправками в уравнении состояния Ван-дер-Ваальса). Область же пространства, приходящая на один атом газа, 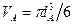 , увеличивается ~
, увеличивается ~ 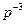 (
(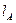 ~
~ 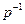 , – диаметр этой области, – среднее расстояние между частицами), когда убыль числа частиц компенсируется соответствующим увеличением объемов, приходящихся на оставшиеся частицы. Очевидно, что в этом случае число всевозможных перемещений, сочетаний и взаимных расположений частиц, оставшихся в меньшем числе, но в прежнем (
, – диаметр этой области, – среднее расстояние между частицами), когда убыль числа частиц компенсируется соответствующим увеличением объемов, приходящихся на оставшиеся частицы. Очевидно, что в этом случае число всевозможных перемещений, сочетаний и взаимных расположений частиц, оставшихся в меньшем числе, но в прежнем (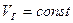 ) объеме, уменьшается – уменьшается их энтропия
) объеме, уменьшается – уменьшается их энтропия 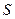 . Уменьшается также и внутренняя энергия
. Уменьшается также и внутренняя энергия 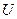 системы частиц: при
системы частиц: при 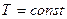 рост
рост 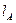 ~
~ 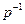 смещает максимум потенциала межчастичного взаимодействия (потенциал Леннарда-Джонса) в область меньших отрицательных энергий. В силу сказанного, с уменьшением числа частиц замкнутой системы (с уменьшением давления газа в ней) уменьшается и суммарная свободная энергия
смещает максимум потенциала межчастичного взаимодействия (потенциал Леннарда-Джонса) в область меньших отрицательных энергий. В силу сказанного, с уменьшением числа частиц замкнутой системы (с уменьшением давления газа в ней) уменьшается и суммарная свободная энергия 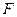 , приходящаяся на оставшиеся частицы.
, приходящаяся на оставшиеся частицы.
|
|
|
IV.4. Возможно ли существование процесса, восстанавливающего (согласно принципу Ле Шателье – Брауна) соотношение 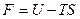 для свободной энергии, характеризующее состояние термодинамического равновесия системы частиц? При
для свободной энергии, характеризующее состояние термодинамического равновесия системы частиц? При 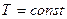 внутренняя энергия системы
внутренняя энергия системы 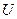 может изменяться только за счет изменения потенциальной энергии взаимодействия частиц – атомов и молекул. Однако эту энергию без напуска газа в объем
может изменяться только за счет изменения потенциальной энергии взаимодействия частиц – атомов и молекул. Однако эту энергию без напуска газа в объем 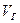 - восстановления в нем прежнего числа частиц и их расстояния между ними – изменить нельзя, –
- восстановления в нем прежнего числа частиц и их расстояния между ними – изменить нельзя, – 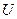 является функцией состояния газа. Энтропия
является функцией состояния газа. Энтропия 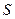 также является функцией состояния газа: при
также является функцией состояния газа: при 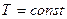 и
и 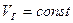 увеличить ее можно также только за счет напуска газа в объем
увеличить ее можно также только за счет напуска газа в объем 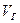 .
.
Без изменения состояния газа, т.е. при 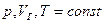 – восстановить
– восстановить 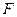 – свободную энергию газового пространства можно только за счет ввода в это пространство дополнительной, свободной энергии, которая будет выполнять роль потенциальной, но только в том случае, если ее изменение, взятое с обратным знаком, равно работе источника при изотермическом процессе [ ].
– свободную энергию газового пространства можно только за счет ввода в это пространство дополнительной, свободной энергии, которая будет выполнять роль потенциальной, но только в том случае, если ее изменение, взятое с обратным знаком, равно работе источника при изотермическом процессе [ ].
Присутствие свободной энергии 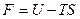 в межатомном (межмолекулярном) пространстве предполагается термодинамическим равновесием воздушной атмосферы при её нормальных условиях,
в межатомном (межмолекулярном) пространстве предполагается термодинамическим равновесием воздушной атмосферы при её нормальных условиях, 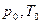 .
.
 2015-10-13
2015-10-13 1082
1082
