III. Почему электрон не может представлять собой поверхностный и объемный

заряд пространства c его плотностью .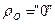

III.1. Математическое определение операции дивергенции предполагает невозможность соотнести распределение заряда электрона с предельно малым объ­ёмом 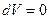. Но тогда очевиден вопрос: пространственное распреде­ление чего, каких зарядов в элементарном объёме 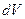образует сток поля 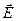и исток поля 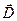? Или иначе: какой элементарный заряд 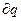в элементарном объёме 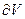сохраняет свою зарядовую плотность истока поля 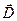с 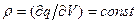? Насколько "эле­ментарный" объём 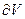элементарен в операциях 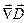и ?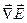

III.2. Определение силы (или обильности) истоков поля 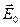через 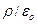и истоков поля 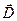через 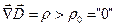требует, чтобы свободный электрон, обладающий энергией 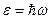и импульсом 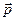= 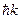, оказавшись на поверхности ПЭ, был каким - то внешним фактором локализован в предельно малом объеме истока, исключающим дробление его заряда 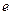. При этом возникает и следующий вопрос: объемное распределение какого заряда в локальной области пространства (газа) становится истоком и стоком поле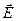й и 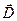? И еще: если не электронов, то заряд чего в своем смещении (по Максвеллу – в буквальном! смысле слова) реализуется в токе смещения 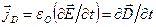и в появлении векторов поле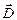й и 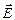? За счёт элементарного объёма 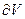чего и в электростатике, и в электродинамике дивергенция поля 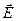остаётся заданной?

III.3. С поступлением импульсного потенциала 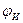на ПЭ распределение зарядов по поверхности 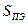ПЭ происходит полевым процессом за 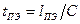, т.е. за время, значительно меньшее, чем вся длительность 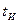импульса 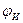. При этом классический подход предполагает, что за 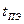кулоновские силы равномерно распределяют электроны по всей длине 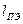поверхности 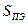. Это обстоятельство позволяет соотнести с зарядом, распределяемым в любой момент времени (в пределах длительности импульса 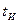) с определенной плотностью 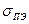по поверхности 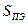ПЭ, поверхностный потенциал 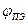и потенциальное, электростатическое поля заряженной поверхности 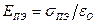с минимум потенциальной энергии, обеспечиваемым устойчивым равновесием системы зарядов на поверхности ПЭ. Однако, согласно теореме Ирншоу [с.96,97], устойчивая статическая конфигурация единичных электрических зарядов невозможна.

III.4. Можно ли соотнести с зарядом, полевым образом распределенным с плотностью 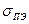по поверхности 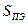, заряд электронов? Пребывания зарядов электронов на 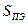в качестве их потенциального распределения предполагает возможность соотнесения с единичным электроном его электростатического, потенциального поля, для определения которого можно использовать, например, теорему Гаусса 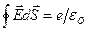. При этом заряд электрона должен быть распределен в объеме пространства 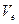, ограниченным поверхностью 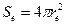, т.е на расстоянии 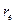от заряда электрона его поле равно 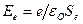при плотности энергии этого поля 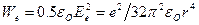. Если за элемент объема 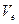принять сферический слой толщиной 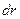и по площади равный 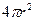, то из 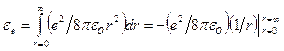можно определить полную энергию в объеме электрона 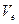. Для точечного заряда (т.е. при интегрировании до 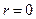) в интеграле получаем бесконечность, которая означает, что, во-первых, представление электрона точечным зарядом (и, как следствие этого, распределение таких зарядов по поверхности ПЭ с плотностью 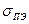) исключается. Во-вторых, если в поле заряда электрона содержится бесконечно много энергии, то это предполагает [7, с.173] возможность существования электрона в качестве пространственного распределения каких-то более элементарных зарядов, чем электрон.

III.5. В экспериментах с разрядом УПГ его развитие в продольном направлении трубки происходит вслед движению по объему газа заряженных образований. В их центральной части с плотностью, определяемой давлением газа, локализован свободный объемный заряд отрицательного знака,СОЗ, который с плотностью этого заряда 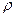в едином объеме может существовать в течение длительного (порядка секунд) времени. Электроны являются фермионами, что исключает возможность их длительного совместного существования, т.е. уравнение непрерывности (неразрывности) заряда 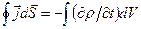не может быть соотнесено с объемным зарядом электронов в объеме СОЗов.

III.6. Статическое распределение свободных единичных электронов по поверхности ПЭ с плотностью их заряда 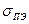несовместимо также с сохранением каждым из них свойств частицы-волны с энергией 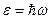и импульсом 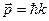[6]. В силу этих же свойств электрона его заряд нельзя соотнести и с предельно малым объемом 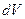в операции дивергенции (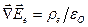), - единичный свободный электрон не может представлять собой силу (или обильность) 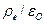истока поля 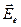как на поверхности ПЭ, так и в объеме газа. По этой же причине электрон не может представлять собой и истоки поля 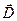(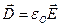), определяемые через 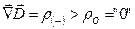, или стоки этого поля с 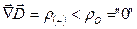, - т.е. и в электростатике, и в электродинамике единичный электрон не может представлять собой заданность дивергенции поле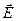й и 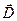, не может представлять плотность энергии потенциального поля пространства 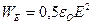(энергия заключена в том пространстве, где имеется электрическое поле и сосредоточена там, где есть заряды, создающее это поле!).

III.7. Поскольку электроны не могут представлять собой заряды такого поля, то возникает основной вопрос этого рассмотрения: какая физическая субстанция, появляющаяся (током 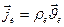) на ПЭ в качестве заряда электронов проводимости в каждый последующий момент времени длительности 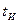импульса 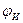распределяется полевым образом (со скоростью С) с плотностью заряда 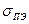по этой поверхности, представляя собой источники полей 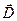, 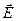и тока смещения ( = = = )?

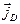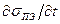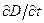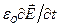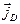III.8. Истоки и стоки поле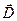й и 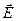появляются в локальной области пространства с его "нулевой" 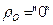зарядовой плотностью при вводе в эту об­ласть (или выводе из нее) током проводимости 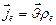сторонних, сво­бодных зарядов извне этой области. Без этих зарядов пространство, заполненное 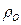, должно представлять собой нейтральную однородную непроводящую среду, обладающую потенциальной возможностьюпоявле­ния в ней заряженной частицы отрицательного знака - электрона, причем независимо от пребывания его в состоянии движения, или по­коя.