I. Зависимые выборки: парные наблюдения.Под случаем зависимых выборок обычно имеют в виду ситуации, в которых речь идет об одном и том же наборе объектов до и после какого-либо воздействия на них. Предполагается, что воздействие может повлиять на признаки, сдвинув их средние значения в большую или в меньшую сторону, и это необходимо проверить. Вначале признаки объектов принимают значения 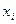 ,после воздействия – значения ,после воздействия – значения 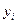 .Такие наблюдения называют парными. Вычисляем их разности .Такие наблюдения называют парными. Вычисляем их разности 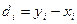 . По наблюдениям . По наблюдениям 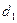 , , 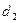 , , 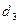 ,.., ,.., 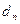 проверяем гипотезу о равенстве нулю генерального среднего ( проверяем гипотезу о равенстве нулю генерального среднего (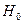 : : 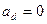 ) при неизвестной дисперсии ) при неизвестной дисперсии 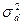 . При этом предполагают, что случайные изменения признаков распределены нормально. Рассмотрите пример 1.Физическая подготовка девяти спортсменов была проверена в баллах при поступлении в спортивную школу ( . При этом предполагают, что случайные изменения признаков распределены нормально. Рассмотрите пример 1.Физическая подготовка девяти спортсменов была проверена в баллах при поступлении в спортивную школу (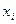 ), а затемпосле недели тренировок ( ), а затемпосле недели тренировок (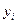 ): ):
Требуется на уровне значимости 0,05 проверить, существенно ли улучшилась подготовка спортсменов (используя нормальное приближение). Решение. Вычисляем разности
Находим: Проверяем гипотезу |
Проверка гипотез для двух выборок. Зависимые выборки: парные наблюдения. Независимые выборки
|
|

Сейчас читают про:
 2015-10-13
2015-10-13 2498
2498
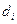
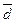 =
= 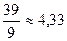 ,
, 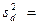 7,94.
7,94.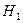 :
: 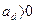 . Находим значение статистики критерия
. Находим значение статистики критерия 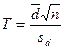 = 1,64. Из таблицы критических точек
= 1,64. Из таблицы критических точек 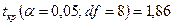 . Поскольку
. Поскольку 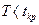 , то нулевая гипотеза принимается. Ответ. Нельзя утверждать, что
, то нулевая гипотеза принимается. Ответ. Нельзя утверждать, что 





